當前位置：試卷中心 > 試卷詳情

2013-2014學年重慶市楊家坪中學高三（上）入學數學試卷（文科）

發布：2024/4/20 14:35:0

1．已知集合M={x|-3＜x＜1，x∈R}，N={-3，-2，-1，0，1}，則M∩N=（　　）
A．{-2，-1，0，1} B．{-3，-2，-1，0} C．{-2，-1，0} D．{-3，-2，-1}
組卷：1502引用：64難度：0.9
解析
2．
|
2
1
+
i
|
=（　　）
A．2
2
B．2 C．
2
D．1
組卷：1401引用：25難度：0.9
解析
3．函數y=
1
log
2
（
x
-
2
）
的定義域為（　　）
A．（-∞，2） B．（2，+∞）
C．（2，3）∪（3，+∞） D．（2，4）∪（4，+∞）
組卷：1934引用：93難度：0.9
解析
4．△ABC的內角A，B，C的對邊分別為a,b,c,已知b=2，B=
π
6
，C=
π
4
，則△ABC的面積為（　　）
A．2
3
+2 B．
3
+
1
C．2
3
-2 D．
3
-1
組卷：5449引用：76難度：0.9
解析
5．已知sin2α=
2
3
，則cos²（α+
π
4
）=（　　）
A．
1
6
B．
1
3
C．
1
2
D．
2
3
組卷：5933引用：93難度：0.7
解析
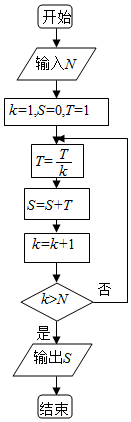6．執行如圖的程序框圖，如果輸入的N=4，那么輸出的S=（　　）
A．1+
1
2
+
1
3
+
1
4
B．1+
1
2
+
1
3
×
2
+
1
4
×
3
×
2
C．1+
1
2
+
1
3
+
1
4
+
1
5
D．1+
1
2
+
1
3
×
2
+
1
4
×
3
×
2
+
1
5
×
4
×
3
×
2
組卷：1371引用：30難度：0.9
解析
7．設a=log₃2，b=log₅2，c=log₂3，則（　　）
A．a＞c＞b B．b＞c＞a C．c＞a＞b D．c＞b＞a
組卷：3899引用：84難度：0.9
解析

20．已知函數
f
（
x
）
=
sin
（
ωx
+
π
6
）
+
sin
（
ωx
-
π
6
）
-
2
co
s
2
ωx
2
，
x
∈
R
（其中ω＞0）
（Ⅰ）求函數f（x）的值域；
（Ⅱ）若函數y=f（x）的圖象與直線y=-1的兩個相鄰交點間的距離為
π
2
，求函數y=f（x）的單調增區間．
組卷：797引用：14難度：0.1
解析
21．已知函數f（x）=x²e^-x
（Ⅰ）求f（x）的極小值和極大值；
（Ⅱ）當曲線y=f（x）的切線l的斜率為負數時，求l在x軸上截距的取值范圍．
組卷：4696引用：20難度：0.1
解析