當前位置：試卷中心 > 試卷詳情

2022-2023學年內蒙古包頭市高一（上）期末數學試卷

發布：2024/4/20 14:35:0

1．已知命題p：?x∈{1，-1，0}，2x+1＞0，則p的否定是（　　）
A．?x∈{1，-1，0}，2x+1≤0 B．?x∈{1，-1，0}，2x+1＞0
C．?x∈{1，-1，0}，2x+1≤0 D．?x∈{1，-1，0}，2x+1＜0
組卷：43引用：2難度：0.8
解析
2．設集合A={n|n=6k+1，k∈Z}，B={n|n=3m+1，m∈Z}，則下列判斷正確的是（　　）
A．A=B B．A∪B=A C．A∩B=A D．B?A
組卷：143引用：3難度：0.9
解析
3．若不等式2kx²+kx-
3
8
＜0對一切實數x都成立，則實數k的取值范圍是（　　）
A．-3＜k＜0 B．-3≤k≤0 C．-3＜k≤0 D．k＜-3或k≥0
組卷：988引用：11難度：0.7
解析
4．已知冪函數f（x）的圖象過點
（
2
，
2
）
，則
f
（
1
2
）
等于（　　）
A．
2
B．
4
C．
2
2
D．
1
4
組卷：36引用：2難度：0.8
解析
5．若0＜a＜1，則函數y=log_a（|x|-1）的圖象可以是（　　）
A． B． C． D．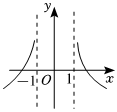
組卷：230引用：5難度：0.8
解析
6．設a=ln2，b=lg0.2，c=e^0.2，則，a,b,c的大小關系為（　　）
A．a＞c＞b B．a＞b＞c C．c＞b＞a D．c＞a＞b
組卷：102引用：2難度：0.9
解析
7．設α是第三象限角，則下列函數值一定為負數的是（　　）
A．cos2α B．
tan
α
2
C．
sin
α
2
D．
cos
α
2
組卷：321引用：6難度：0.8
解析

21．為迎接2022年“雙十一”網購狂歡節，某廠家擬投入適當的廣告費，對網上所售產品進行促銷．經調查測算，該促銷產品在“雙十一”的銷售量p萬件與促銷費用x萬元滿足：
p
=
4
-
3
x
+
1
（其中0≤x≤a,a為正常數）．已知生產該產品還需投入成本（10+2p）萬元（不含促銷費用），產品的銷售價格定為
（
5
+
20
p
）
元/件．假定廠家的生產能力完全能滿足市場的銷售需求．
（1）將該產品的利潤y萬元表示為促銷費用x萬元的函數；
（2）促銷費用投入多少萬元時，廠家的利潤最大？并求出最大利潤的值．
組卷：34引用：2難度：0.6
解析
22．設函數f（x）=-2^x+2^-x（x∈R）．
（1）若存在x∈[0，1]，使得2^x?f（x）-4?2^x+m≤0成立，求實數m的最大值；
（2）設函數h（x）=2^x+2^-x，g（x）=λf（x）+h（2x）+2，若g（x）在[1，+∞）上有兩個零點，求實數λ的取值范圍．
組卷：29引用：3難度：0.5
解析