當前位置：試卷中心 > 試卷詳情

2022-2023學年福建省漳州市華安縣八年級（下）期中數學試卷

發布：2024/5/3 8:0:9

一、選擇題：本題共10小題，每小題4分，共40分．

1．如圖，如圖化學分子結構模型平面圖中，是中心對稱圖形的是（　　）
A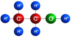． B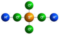． C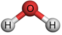． D．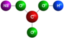
組卷：39引用：3難度：0.9
解析
2．如果分式
x
-
1
x
+
1
在實數范圍內有意義，則x的取值范圍是（　　）
A．x≠1 B．x=-1 C．全體實數 D．x≠-1
組卷：144引用：3難度：0.8
解析
3．華為Mate20手機搭載了全球首款7納米制程芯片，7納米就是0.000000007米．數據0.000000007用科學記數法表示為（　　）
A．0.7×10^-8 B．7×10^-7 C．7×10^-8 D．7×10^-9
組卷：537引用：27難度：0.9
解析
4．若一次函數y=（a-2）x-b的圖象中y值隨x值的增大而增大，則a的值可以是（　　）
A．4 B．2 C．-2 D．-6
組卷：873引用：5難度：0.7
解析
5．如圖，?ABCD的對角線AC，BD相交于點O，且AC+BD=16，若△BCO的周長為14，則BC的長是（　　）
A．12 B．9 C．8 D．6
組卷：334引用：6難度：0.7
解析
6．在反比例函數y=
1
-
m
x
的圖象的每一條曲線上，y都隨x的增大而減小，則m的值可以是（　　）
A．0 B．1 C．2 D．3
組卷：257引用：8難度：0.9
解析
7．直線y=kx-2一定經過點（　　）
A．（2，0） B．（2，k） C．（0，k） D．（0，-2）
組卷：180引用：2難度：0.5
解析
8．數學家斐波那契編寫的《算經》中有如下分錢問題：第一次由一組人平分10元錢，每人分得若干，第二次比第一次增加6人，平分40元錢，則第二次每人分得的錢與第一次相同，設第二次分錢的人數為x人，則可列方程為（　　）
A．10x=40（x+6） B．10（x-6）=40x
C．
10
x
=
40
x
+
6
D．
10
x
-
6
=
40
x
組卷：132引用：2難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：本題共9小題，共86分，解答應寫出文字說明、證明過程或演算步驟

24．閱讀下列材料：
材料1：在處理分數和分式問題時，有時由于分子比分母大，或者分子的次數高于分母的次數，在實際運算時往往難度比較大，這時我們可以將假分數（分式）拆分成一個整數（整式）與一個真分數（式）的和（差）的形式，通過對簡單式的分析來解決問題，我們稱之為分離整數法．此法在處理分式或整除問題時頗為有效．如將分式
x
2
-
3
x
-
1
x
+
2
拆分成一個整式與一個分式（分子為整數）的和的形式．
解：設x+2=t,則x=t-2．∴原式
（
t
-
2
）
2
-
3
（
t
-
2
）
-
1
t
=
t
2
-
7
t
+
9
t
=t-7+
9
t

∴
x
2
-
3
x
-
1
x
+
2
=x-5+
9
x
+
2

材料2：配方法是初中數學思想方法中的一種重要的解題方法，配方法最終的目的就是配成完全平方式，利用完全平方式來求解，它的應用非常廣泛，在解方程、求最值、證明等式、化簡根式、因式分解等方面都經常用到．如：當a＞0，b＞0時，∵
a
b
+
b
a
=（
a
b
）²+（
b
a
）²=（
a
b
-
b
a
）²+2
∴當
a
b
=
b
a
，即a=b時，
a
b
+
b
a
有最小值2．
根據以上閱讀材料回答下列問題：
（1）將分式
x
2
+
x
+
3
x
+
1
拆分成一個整式與一個分子為整數的分式的和的形式，則結果為
；
（2）已知分式
4
x
2
-
10
x
+
8
2
x
-
1
的值為整數，求整數x的值；
（3）當-1＜x＜1時，求代數式
-
12
x
4
+
14
x
2
-
5
-
2
x
2
+
2
的最大值及此時x的值．
組卷：387引用：4難度：0.4
解析
25．如圖，在平面直角坐標系xOy中，直線y=-x+4分別交x軸、y軸于點A、點B，點C在x軸的負半軸上，且OC=
1
2
OB，點P是線段BC上的動點（點P不與B，C重合），以BP為斜邊在直線BC的右側作等腰直角三角形BPD．
（1）求直線BC的函數表達式；
（2）如圖1，當S_△BPD=
3
20
S_△ABC時，求點P的坐標；
（3）如圖2，連接AP，點E是線段AP的中點，連接DE，OD．試探究∠ODE的大小是否為定值，若是，求出∠ODE的度數；若不是，請說明理由．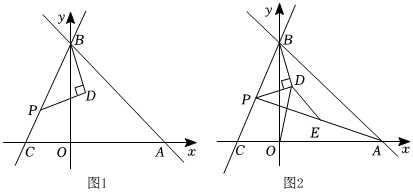
組卷：1142引用：7難度：0.2
解析