2010年重慶市萬州區初中數學教師專業知識競賽試卷
發布:2024/4/20 14:35:0
一、選擇題(共5小題,每小題2分,滿分10分)
-
1.下列各式計算正確的是( )
A.2a2+a3=3a5 B.(3xy)2÷(xy)=3xy C.(2b2)3=8b5 D.2x?3x5=6x6 組卷:364引用:61難度:0.9 -
 2.某幾何體的三種視圖如圖所示,則該幾何體可能是( )
2.某幾何體的三種視圖如圖所示,則該幾何體可能是( )A.圓錐體 B.球體 C.長方體 D.圓柱體 組卷:41引用:21難度:0.9 -
3.下列命題為真命題的是( )
A.三角形的中位線把三角形的面積分成相等的兩部分 B.對角線相等且相互平分的四邊形是正方形 C.關于某直線對稱的兩個三角形是全等三角形 D.一組對邊平行,另一組對邊相等的四邊形一定是等腰梯形 組卷:33引用:12難度:0.9 -
4.如圖,把圖1中的△ABC經過一定的變換得到圖2中的△A′B′C′,如果圖1中△ABC上點P的坐標為(a,b),那么這個點在圖2中的對應點P′的坐標為( )

A.(a-2,b-3) B.(a-3,b-2) C.(a+3,b+2) D.(a+2,b+3) 組卷:901引用:48難度:0.9 -
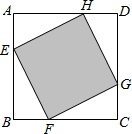 5.如圖,已知:正方形ABCD邊長為1,E、F、G、H分別為各邊上的點,且AE=BF=CG=DH,設小正方形EFGH的面積為s,AE為x,則s關于x的函數圖象大致是( )
5.如圖,已知:正方形ABCD邊長為1,E、F、G、H分別為各邊上的點,且AE=BF=CG=DH,設小正方形EFGH的面積為s,AE為x,則s關于x的函數圖象大致是( )A. 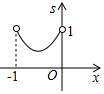
B. 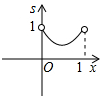
C. 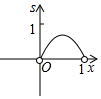
D. 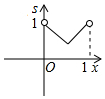 組卷:6240引用:124難度:0.5
組卷:6240引用:124難度:0.5
二、填空題(共9小題,滿分30分)
-
6.計算:20+2-1=.
組卷:273引用:25難度:0.7
三、解答題(共10小題,滿分60分)
-
18.2008年8月,北京奧運會帆船比賽將在青島國際帆船中心舉行.觀看帆船比賽的船票分為兩種:A種船票600元/張,B種船票120元/張.某旅行社要為一個旅行團代購部分船票,在購票費不超過5000元的情況下,購買A,B兩種船票共15張,要求A種船票的數量不少于B種船票數量的一半.若設購買A種船票x張,請你解答下列問題:
(1)共有幾種符合題意的購票方案寫出解答過程;
(2)根據計算判斷:哪種購票方案更省錢?組卷:365引用:44難度:0.3 -
19.根據所給的基本材料,請你進行適當的處理,編寫一道綜合題.
編寫要求:①提出具有綜合性、連續性的三個問題;②給出正確的解答過程;③寫出編寫意圖和學生答題情況的預測.
材料①:如圖,先把一矩形紙片ABCD對折,得到折痕MN,然后把B點疊在折痕線上,得到△ABE,再過點B把矩形ABCD第三次折疊,使點D落在直線AD上,得到折痕PQ.當沿著BE第四次將該紙片折疊后,點A就會落在EC上.
材料②:已知AC是∠MAN的平分線.
(1)在圖1中,若∠MAN=120°,∠ABC=ADC=90°,求證:AB+AD=AC;
(2)在圖2中,若∠MAN=120°,∠ABC+∠ADC=180°,則(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請說明理由;
(3)在圖3中:若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,
則AB+AD=AC(用含α的三角函數表示).
材料③:
已知:如圖甲,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,點P由B出發沿線段BA向點A勻速運動,速度為1cm/s;點Q由A出發沿線段AC向點C勻速運動,速度為2cm/s;連接PQ,設運動的時間為t(s)(0<t<2).
編寫試題選取的材料是(填寫材料的序號)
編寫的試題是:(1)設△AQP的面積為y(cm2),求y與t之間的函數關系式.
(2)是否存在某一時刻t,使線段PQ恰好把Rt△ACB的周長和面積同時平分?若存在,求出此時t的值.
(3)如圖(2),連接PC,并把△PQC沿QC翻折得到四邊形PQP'C.是否存在某一時刻t,使四邊形PQP'C為菱形?若存在,求出此時菱形的邊長.
試題解答(寫出主要步驟即可):(1)過點Q作QD⊥AP于點D,證△AQD∽△ABC,利用相似性質及面積解答;
(2)分別求得Rt△ACB的周長和面積,由周長求出t,代入函數解析式驗證;
(3)利用余弦定理得出PC、PQ,聯立方程,求得t,再代入PC解得答案.組卷:354引用:1難度:0.5


