當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年四川省成都市蓉城聯(lián)盟高二（下）期中數(shù)學(xué)試卷

發(fā)布：2024/11/19 9:30:2

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

1．已知集合
A
=
{
y
|
y
=
x
}
，B={y|y=cosx,x∈R}，則A∩B=（　　）
A．[-1，1] B．[0，1] C．[0，+∞） D．（0，+∞）
組卷：27引用：3難度：0.8
解析
2．已知角
α
∈
（
3
π
2
，
2
π
）
，
cosα
=
4
5
，則
cos
（
π
4
-
α
）
=（　　）
A．
-
7
2
10
B．
7
2
10
C．
-
2
10
D．
2
10
組卷：77引用：3難度：0.7
解析
3．下列函數(shù)是偶函數(shù)且在
（
0
，
π
2
）
上單調(diào)遞增的是（　　）
A．y=sinx B．y=cosx C．y=tanx D．y=|sinx|
組卷：18引用：3難度：0.7
解析
4．若f（x）=cos（2x+φ）（0＜φ＜π）為奇函數(shù)，則φ=（　　）
A．
π
6
B．
π
3
C．
π
2
D．
3
π
4
組卷：190引用：3難度：0.8
解析
5．如圖，點(diǎn)O為正六邊形ABCDEF的中心，下列說(shuō)法正確的是（　　）
A．
AB
=
OD
B．
|
EF
|
=
|
AB
|
C．
AB
與
AD
共線 D．
BE
＞
BC
組卷：141引用：4難度：0.7
解析
6．已知角x為斜三角形的內(nèi)角，
f
（
x
）
=
3
tanx
-
3
，則f（x）≥0的x的取值范圍是（　　）
A．
[
π
6
，
π
）
B．
[
π
3
，
π
）
C．
[
π
6
，
π
2
）
D．
[
π
3
，
π
2
）
組卷：19引用：3難度：0.7
解析
7．函數(shù)
f
（
x
）
=
cos
2
x
+
4
cos
（
π
2
+
x
）
的最大值為（　　）
A．
1
2
B．1 C．3 D．4
組卷：106引用：3難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題：本題共6小題，共70分．解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

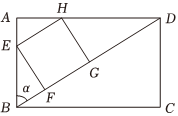21．中國(guó)剪紙是一種用剪刀或刻刀在紙上剪刻花紋，用于裝點(diǎn)生活或配合其他民俗活動(dòng)的民間藝術(shù)．在中國(guó)，剪紙具有廣泛的群眾基礎(chǔ)，交融于各族人民的社會(huì)生活，是名種民俗活動(dòng)的重要組成部分，傳承視覺(jué)形象和造型格式，蘊(yùn)涵了豐富的文化歷史信息，表達(dá)了廣大民眾的社會(huì)認(rèn)知、道德觀念、實(shí)踐經(jīng)驗(yàn)、生活理想和審美情趣．現(xiàn)有一張矩形卡片ABCD，對(duì)角線長(zhǎng)為t（t為常數(shù)），從△ABD中裁出一個(gè)內(nèi)接正方形紙片EFGH，使得點(diǎn)E，H分別AB，AD上，設(shè)
∠
DBA
=
α
（
0
＜
α
＜
π
2
）
，矩形紙片ABCD的面積為S₁，正方形紙片EFGH的面積為S₂．
（1）當(dāng)
α
=
5
π
12
時(shí)，求正方形紙片EFGH的邊長(zhǎng)（結(jié)果用t表示）；
（2）當(dāng)α變化時(shí)，求
S
2
S
1
的最大值及對(duì)應(yīng)的α值．
組卷：87引用：6難度：0.6
解析
22．已知
f
（
x
）
=
sin
（
x
+
π
6
）
+
sin
（
x
-
π
3
）
．
（1）當(dāng)x∈R時(shí)，求f（x）≥1的x的取值范圍；
（2）是否存在實(shí)數(shù)k,使得不等式
f
（
2
x
+
π
12
）
+
（
k
-
4
）
f
（
x
+
π
12
）
+
（
k
-
4
）
f
（
x
+
7
π
12
）
＜
3
2
，對(duì)任意的
x
∈
[
-
π
2
，
π
2
]
恒成立，若存在，求出k的取值范圍；若不存在，請(qǐng)說(shuō)明理由．
組卷：42引用：4難度：0.5
解析