2010年上海市“新知杯”初中數學競賽試卷

一、填空題（共10小題，每小題8分，滿分80分）

• 1．已知

  x

  +

  1

  x

  =

  3

  ，則

  x

  10

  +

  x

  5

  +

  1

  x

  5

  +

  1

  x

  10

  =

   

  ．
  組卷：162引用：1難度：0.9

  解析

• 2．滿足方程（x+3）²+y²+（x-y）²=3的所有實數對（x,y）為

  ．
  組卷：124引用：1難度：0.9

  解析

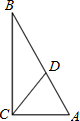• 3．已知直角三角形ABC中，∠C=90°，BC=6，CA=3，CD為∠C的角平分線，則CD=

  ．
  組卷：301引用：1難度：0.7

  解析

• 4．若前2011個正整數的乘積1×2×…×2011能被2010^k整除，則 正整數k的最大值為

   

  ．
  組卷：157引用：1難度：0.5

  解析

二、解答題（共4小題，滿分60分）

• 13．設實數x,y,z滿足x+y+z=0，且（x-y）²+（y-z）²+（z-x）²≤2，求x的最大值和最小值．
  組卷：255引用：1難度：0.1

  解析

• 14．稱具有a²+161b²形式的數為“好數”，其中a,b都是整數．
  （1）證明：100，2010都是“好數”．
  （2）證明：存在正整數x,y,使得x¹⁶¹+y¹⁶¹是“好數”，而x+y不是“好數”．
  組卷：125引用：1難度：0.1

  解析