2022-2023學年湖北省荊門市東寶中學高二（上）期中數學試卷

一、單選題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．直線x+

  3

  y+1=0的傾斜角是（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：1042引用：97難度：0.9

  解析

• 2．圓x²+y²-2x+4y+1=0的半徑為（　　）

  A．1

  B． 2

  C．2

  D．4
  組卷：98引用：5難度：0.9

  解析

• 3．已知向量

  a

  =（0，1，1），

  b

  =（1，-2，1）．若向量

  a

  +

  b

  與向量

  c

  =（-2，m,-4）平行，則實數m的值是（　　）

  A．2

  B．-2

  C．10

  D．-10
  組卷：454引用：4難度：0.7

  解析

• 4．同時拋擲兩枚骰子，向上點數之和為5的概率是（　　）

  A． 1 9

  B． 2 21

  C． 1 18

  D． 1 6
  組卷：32引用：11難度：0.9

  解析

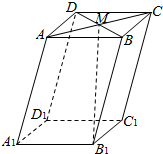• 5．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為AC與BD的交點，若

  A

  1

  B

  1

  =

  a

  ，

  A

  1

  D

  1

  =

  b

  ，

  A

  1

  A

  =

  c

  ．則下列向量中與

  B

  1

  M

  相等的向量是（　　）

  A．- 1 2 a + 1 2 b + c

  B． 1 2 a + 1 2 b + c

  C． 1 2 a - 1 2 b + c

  D．- 1 2 a - 1 2 b + c
  組卷：1928引用：110難度：0.9

  解析

• 6．有5個條件類似的大學畢業生A，B，C，D，E應聘某兩個相同的工作崗位，每個崗位只招聘1人，如果每個人被錄用的機會相等，則學生A被錄用的概率為（　　）

  A． 4 5

  B． 3 5

  C． 2 5

  D． 1 5
  組卷：162引用：3難度：0.8

  解析

• 7．已知圓C₁：x²+y²=a關于直線l對稱的圓為圓C₂：x²+y²+2x-2ay+3=0，則直線l的方程為（　　）

  A．2x-4y+5=0

  B．2x+4y+5=0

  C．2x-4y-5=0

  D．2x+4y-5=0
  組卷：582引用：4難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

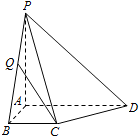• 21．如圖，在四棱錐P-ABCD中，已知PA⊥平面ABCD，且四邊形ABCD為直角梯形，∠ABC=∠BAD=

  π

  2

  ，PA=AD=2，AB=BC=1．
  （1）求平面PAB與平面PCD所成二面角的余弦值；
  （2）點Q是線段BP上的動點，當直線CQ與DP所成的角最小時，求線段BQ的長．
  組卷：3630引用：22難度：0.3

  解析

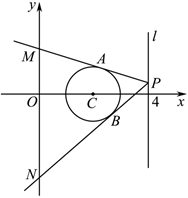• 22．如圖，圓C：（x-2）²+y²=1，點P為直線l：x=4上一動點，過點P引圓C的兩條切線，切點分別為A，B．
  （1）（i）設點P（4，t），求△PAB外接圓的方程；
  （ii）求證：直線AB恒過定點，并求出該定點Q的坐標；
  （2）若兩條切線PA，PB于y軸分別交于M，N兩點，求△QMN面積的最小值．
  組卷：86引用：2難度：0.5

  解析