2022-2023學年湖南省益陽市六校高二（上）期末數學試卷

一、選擇題（共40分）

• 1．已知向量

  a

  =（1，2，-2），

  b

  =（-3，-6，6），

  c

  =（2，1，2）則它們的位置關系是（　　）

  A． a ∥ b ， a ∥ c

  B． a ⊥ b ， a ⊥ c

  C． a ⊥ b ， b ∥ c

  D． a ∥ b ， b ⊥ c
  組卷：400引用：2難度：0.7

  解析

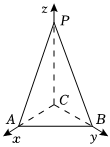• 2．在三棱錐P-ABC中，CP，CA，CB兩兩互相垂直，AC=CB=1，PC=2，建立如圖所示的空間直角坐標系，則下列向量是平面PAB的一個法向量的是（　　）

  A． （ 1 ， 1 ， 1 2 ）

  B． （ 1 ， 2 ， 1 ）

  C．（1，1，1）

  D．（2，-2，1）
  組卷：511引用：4難度：0.7

  解析

• 3．已知等比數列{a_n}的公比為q,前n項和為S_n，若q=2，S₂=6，則S₃=（　　）

  A．8

  B．10

  C．12

  D．14
  組卷：217引用：6難度：0.7

  解析

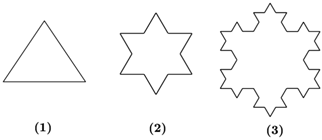
• 4．如圖，將一個邊長為1的正三角形的每條邊三等分，以中間一段為邊向外作正三角形，并擦去中間一段，得圖（2），如此繼續下去，得圖（3）…，設第n個圖形的邊長為a_n，則數列{a_n}的通項公式為（　　）

  A． 1 3 n

  B． 1 3 n - 1

  C． 1 3 n

  D． 1 3 n - 1
  組卷：37引用：1難度：0.7

  解析

• 5．數學家歐拉在1765年發現，任意三角形的外心、重心、垂心位于同一條直線上，這條直線稱為歐拉線．已知△ABC的頂點A（2，0），B（0，4），若其歐拉線的方程為x-y+2=0，則頂點C的坐標為（　　）

  A．（-4，0）

  B．（-3，-1）

  C．（-5，0）

  D．（-4，-2）
  組卷：1054引用：17難度：0.6

  解析

• 6．已知定點B（3，0），點A在圓（x+1）²+y²=4上運動，則線段AB的中點M的軌跡方程是（　　）

  A．（x+1）2+y2=1	B．（x-2）2+y2=4
  C．（x-1）2+y2=1	D．（x+2）2+y2=4
  組卷：313引用：8難度：0.7

  解析

• 7．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  ，F₁，F₂分別是雙曲線的左、右焦點，M是雙曲線右支上一點，連接MF₁交雙曲線C左支于點N，若△MNF₂是以F₂為直角頂點的等腰直角三角形，則雙曲線的離心率為（　　）

  A． 2

  B． 3

  C．2

  D． 5
  組卷：174引用：5難度：0.5

  解析

四、解答題（共70分）

• 21．已知圓C過點M（0，-2），N（3，1），且圓心C在直線x+2y+1=0上．
  （1）求圓C的標準方程；
  （2）設直線ax-y+1=0與圓C交于不同的兩點A，B，是否存在實數a,使得過點P（2，0）的直線l垂直平分弦AB？若存在，求出實數a的值；若不存在，請說明理由．
  組卷：202引用：7難度：0.5

  解析

• 22．已知橢圓C的離心率為

  3

  2

  ，長軸的兩個端點分別為A（-2，0），B（2，0）．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）過點（1，0）的直線與橢圓C交于M，N（不與A，B重合）兩點，直線AM與直線x=4交于點Q．求證：

  S

  △

  MBN

  S

  △

  MBQ

  =

  |

  BN

  |

  |

  BQ

  |

  ．
  組卷：407引用：4難度：0.5

  解析