2022-2023學年廣東省深圳市南山區蛇口育才教育集團育才中學高一（上）期末數學試卷

一、單選題（本大題共8小題，共40.0分。在每小題列出的選項中，選出符合題目的一項）

• 1．若集合A={x|x²-3x≤0}，集合B={x|1≤x＜5}，則A∪B=（　　）

  A．{x|x＜5}

  B．{x|1≤x≤3}

  C．{x|0≤x＜5}

  D．{x|3≤x＜5}
  組卷：102引用：2難度：0.7

  解析

• 2．如果角θ的終邊經過點（-

  3

  2

  ，

  1

  2

  ），則cosθ=（　　）

  A．- 3 3

  B．- 3 2

  C． 1 2

  D． 3
  組卷：368引用：10難度：0.9

  解析

• 3．如果冪函數y=x^α的圖象經過點（2，

  1

  4

  ），那么α等于（　　）

  A．-2

  B．2

  C． - 1 2

  D． 1 2
  組卷：203引用：5難度：0.9

  解析

• 4．下列不等式中成立的是（　　）

  A．若a＞b＞0，則ac2＞bc2	B．若a＞b＞0，則a2＞b2
  C．若a＜b＜0，則a2＜ab＜b2	D．若a＜b＜0，則 1 a ＜ 1 b
  組卷：1028引用：31難度：0.8

  解析

• 5．函數f（x）=

  ln

  |

  x

  |

  x

  的圖象大致形狀是（　　）

  A．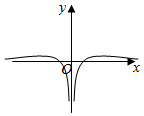

  B．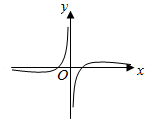

  C．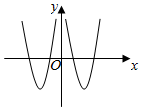

  D．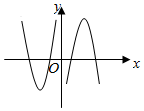
  組卷：223引用：9難度：0.7

  解析

• 6．當x越來越大時，下列函數中，增長速度最快的應是（　　）

  A．y=5x

  B．y=log5x

  C．y=x5

  D．y=5x
  組卷：186引用：4難度：0.8

  解析

• 7．函數f（x）在（0，+∞）單調遞增，且f（x+3）關于x=-3對稱，若f（-2）=1，則f（x-2）≤1的x的取值范圍是（　　）

  A．[-2，2]	B．（-∞，-2]∪[2，+∞）
  C．（-∞，0]∪[4，+∞）	D．[0，4]
  組卷：276引用：5難度：0.7

  解析

四、解答題（本大題共6小題，共70.0分。解答應寫出文字說明，證明過程或演算步驟）

• 21．設函數

  f

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  4

  ）

  ，

  x

  ∈

  R

  ．
  （1）求函數f（x）的最小正周期和單調遞增區間；
  （2）求函數f（x）在區間

  [

  π

  8

  ，

  3

  π

  4

  ]

  上的最小值和最大值，并求出取最值時x的值．
  組卷：1514引用：20難度：0.3

  解析

• 22．已知函數f（x）=x²+（m-2）x-m,

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  x

  ，且函數y=f（x-2）是偶函數．
  （1）求g（x）的解析式；
  （2）若不等式g（lnx）-nlnx≥0在

  [

  1

  e

  2

  ，

  1

  ）

  上恒成立，求n的取值范圍；
  （3）若函數

  y

  =

  g

  （

  log

  2

  （

  x

  2

  +

  4

  ）

  ）

  +

  k

  ?

  2

  log

  2

  （

  x

  2

  +

  4

  ）

  -

  9

  恰好有三個零點，求k的值及該函數的零點．
  組卷：366引用：13難度：0.3

  解析