2022-2023學年廣東省佛山市順德一中高二（上）第一次月考數學試卷

一、單選題（每題6分，共48分）

• 1．已知向量

  AB

  =

  （

  2

  ，

  4

  ，

  x

  ）

  ，平面α的一個法向量

  n

  =

  （

  1

  ，

  y

  ,

  3

  ）

  ，若AB∥α，則（　　）

  A．x=6，y=2

  B．x=2，y=6

  C．3x+4y+2=0

  D．4x+3y+2=0
  組卷：105引用：3難度：0.8

  解析

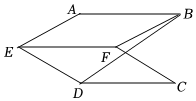• 2．如圖所示，在大小為30°的二面角A-EF-D中，四邊形ABFE和四邊形CDEF都是邊長為1的正方形，則B，D兩點間的距離是（　　）

  A．2

  B． 2

  C． 3 - 3

  D． 3 + 3
  組卷：87引用：2難度：0.6

  解析

• 3．平行六面體ABCD-A₁B₁C₁D₁中AB=2，AD=2，AA₁=3，∠DAB=∠BAA₁=∠DAA₁=60°，則該平行六面體的體對角線AC₁的長為（　　）

  A． 33

  B．5

  C． 24

  D． 17
  組卷：43引用：4難度：0.5

  解析

• 4．已知矩形ABCD，P為平面ABCD外一點，且PA⊥平面ABCD，M，N分別為PC，PD上的點，且

  NM

  =x

  AB

  +y

  AD

  +z

  AP

  ，

  PM

  =2

  MC

  ，

  PN

  =

  ND

  ，則x+y+z的值為（　　）

  A． - 2 3

  B． 2 3

  C．1

  D． 5 6
  組卷：307引用：7難度：0.6

  解析

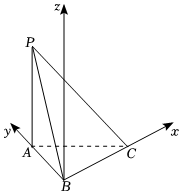• 5．如圖，在三棱錐P-ABC中，PA⊥平面ABC，∠ABC=90°，∠BAC=60°，PA=AB=2，以B為原點，分別以

  BC

  ，

  BA

  ，

  AP

  的方向為x軸，y軸，z軸的正方向建立空間直角坐標系，設平面PAB和平面PBC的一個法向量分別為

  m

  ，

  n

  ，則下列結論中正確的是（　　）

  A．點P的坐標為（0，0，2）	B． PC = （ 4 ， 0 ，- 2 ）
  C． cos ? m ， n ? ＞ 0	D． n = （ 0 ，- 2 ， 2 ）
  組卷：109引用：7難度：0.7

  解析

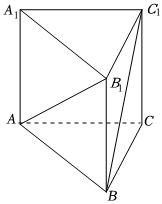• 6．如圖，在正三棱柱ABC-A₁B₁C₁中，若AB=

  2

  B

  B

  1

  ，則AB₁與BC₁所成角的大小為（　　）

  A．60°

  B．90°

  C．105°

  D．75°
  組卷：546引用：20難度：0.7

  解析

四、解答題

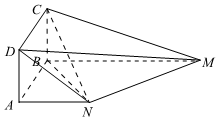• 19．如圖所示，正方形ABCD所在平面與梯形ABMN所在平面垂直，MB∥AN，NA=AB=2，BM=4，CN=2

  3

  ．
  （1）證明：DN∥平面BCM；
  （2）求直線AC與平面CDM所成角的正弦值；
  （3）在線段CM上是否存在一點E，使得平面BEN與平面BMN的夾角的余弦值為

  3

  3

  ，若存在，求出

  CE

  EM

  的值，若不存在，請說明理由．
  組卷：169引用：3難度：0.5

  解析

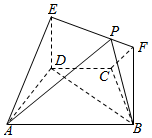• 20．如圖，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠BCD=120°，四邊形BFED為矩形，平面BFED⊥平面ABCD，BF=1．
  （Ⅰ）求證：AD⊥平面BFED；
  （Ⅱ）點P是線段EF上運動，設平面PAB與平面ADE成銳角二面角為θ，試求θ的最小值．
  組卷：182引用：14難度：0.5

  解析