2023-2024學(xué)年廣東省肇慶中學(xué)大旺實驗學(xué)校高二（上）開學(xué)數(shù)學(xué)試卷

一、單選題（本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的。）

• 1．復(fù)數(shù)

  5

  2

  -

  i

  =（　　）

  A．2+i

  B．-2+i

  C．-2-i

  D．2-i
  組卷：112引用：5難度：0.8

  解析

• 2．甲、乙同時參加某次法語考試，甲、乙考試達到優(yōu)秀的概率分別為0.6，0.7，兩人考試相互獨立，則甲、乙兩人都未達到優(yōu)秀的概率為（　　）

  A．0.42

  B．0.28

  C．0.18

  D．0.12
  組卷：220引用：5難度：0.8

  解析

• 3．若一組樣本數(shù)據(jù)x₁，x₂，…，x_n的方差為0.01，則數(shù)據(jù)4x₁+1，4x₂+1，4x₃+1，…，4x_n+1的方差為（　　）

  A．0.04

  B．0.16

  C．1.04

  D．1.16
  組卷：186引用：2難度：0.8

  解析

• 4．在△ABC中，角A，B，C的對邊分別是a,b,c,若

  a

  =

  3

  ，

  c

  =

  8

  ，

  B

  =

  π

  3

  ，則b=（　　）

  A．6

  B．7

  C． 61

  D． 95
  組卷：191引用：4難度：0.7

  解析

• 5．已知點A（1，-1，2）關(guān)于y軸的對稱點為B，則|AB|=（　　）

  A． 2 5

  B． 2 6

  C．2

  D． 3 2
  組卷：159引用：2難度：0.7

  解析

• 6．P是△ABC所在平面內(nèi)一點，若

  CB

  =λ

  PA

  +

  PB

  ，其中λ∈R，則P點一定在（　　）

  A．△ABC內(nèi)部	B．AC邊所在直線上
  C．AB邊所在直線上	D．BC邊所在直線上
  組卷：916引用：26難度：0.7

  解析

• 7．已知向量

  a

  =（k,3），

  b

  =（1，4），

  c

  =（2，1）且（2

  a

  -3

  b

  ）⊥

  c

  ，則實數(shù)k=（　　）

  A．- 9 2

  B．0

  C．3

  D． 15 2
  組卷：4262引用：74難度：0.9

  解析

四、解答題（本大題共6大題，共70分，解答應(yīng)寫出文字說明、證明過程或演算步驟．）

• 21．記鈍角△ABC的內(nèi)角A，B，C的對邊分別為a,b,c,已知

  cos

  A

  1

  -

  sin

  A

  =

  cos

  A

  +

  cos

  B

  1

  -

  sin

  A

  +

  sin

  B

  ．
  （1）若

  C

  =

  2

  π

  3

  ，求A；
  （2）求

  a

  2

  +

  c

  2

  b

  2

  的取值范圍．
  組卷：115引用：3難度：0.5

  解析

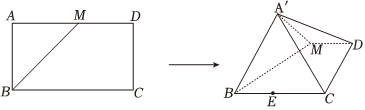• 22．如圖，在矩形ABCD中，AB=1，

  BC

  =

  3

  ，M是線段AD上的一動點，將△ABM沿著BM折起，使點A到達點A'的位置，滿足點A'?平面BCDM且點A'在平面BCDM內(nèi)的射影E落在線段BC上．
  （1）當(dāng)點M與端點D重合時，證明：A'B⊥平面A'CD；
  （2）求三棱錐E-A'BM的體積的最大值；
  （3）設(shè)直線CD與平面A'BM所成的角為α，二面角A'-BM-C的平面角為β，求2sinα?cosβ的最大值．
  組卷：30引用：1難度：0.4

  解析