當前位置：試卷中心 > 試卷詳情

2020-2021學年吉林省松原市長嶺二中高三（上）期末數學試卷（文科）

發布：2024/4/20 14:35:0

1．設集合A={x|x²-4x+3＜0}，B={x|2x-3＞0}，則A∩B=（　　）
A．（-3，-
3
2
） B．（-3，
3
2
） C．（1，
3
2
） D．（
3
2
，3）
組卷：10170引用：84難度：0.9
解析
2．下列函數中，既是偶函數又在（-∞，0）上單調遞增的函數是（　　）
A．y=x² B．y=2^|x| C．
y
=
ln
1
|
x
|
D．y=xcosx
組卷：83引用：5難度：0.9
解析
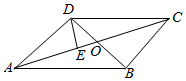3．如圖在平行四邊形ABCD中，對角線AC與BD交于點O，且
AE
=2
EO
，則
ED
=（　　）
A．
1
3
AD
-
2
3
AB
B．
2
3
AD
+
1
3
AB
C．
2
3
AD
-
1
3
AB
D．
1
3
AD
+
2
3
AB
組卷：887引用：20難度：0.8
解析
4．在等差數列{a_n}中，已知a₄+a₈=16，則該數列前11項和S_n=（　　）
A．58 B．88 C．143 D．176
組卷：16引用：1難度：0.7
解析
5．已知平面向量
a
、
b
，滿足|
a
|=|
b
|=1，若（2
a
-
b
）?
b
=0，則向量
a
、
b
的夾角為（　　）
A．30° B．45° C．60° D．120°
組卷：302引用：15難度：0.8
解析
6．已知點A（-1，0）、B（1，3），向量
a
=（2k-1，2），若
AB
⊥
a
，則實數k的值為（　　）
A．-2 B．-1 C．1 D．2
組卷：112引用：36難度：0.9
解析
7．若cos（
π
4
-
θ
）=
1
2
，則sin2θ=（　　）
A．-
1
2
B．-
3
2
C．
1
2
D．
3
2
組卷：235引用：8難度：0.7
解析

21．已知數列{a_n}的前n項和是S_n，且S_n
+
1
2
a
n
=1（n∈N），數列{b_n}是公差d不等于0的等差數列，且滿足：b₁=
3
2
a
1
，b₂，b₅，b₁₄成等比數列．
（Ⅰ）求數列{a_n}、{b_n}的通項公式；
（Ⅱ）設c_n=a_n?b_n，求數列{c_n}的前n項和T_n．
組卷：1526引用：9難度：0.3
解析
22．設函數f（x）=[ax²-（3a+1）x+3a+2]e^x．
（Ⅰ）若曲線y=f（x）在點（2，f（2））處的切線斜率為0，求a；
（Ⅱ）若f（x）在x=1處取得極小值，求a的取值范圍．
組卷：4053引用：14難度：0.3
解析