2022年遼寧省高考數學聯考試卷（3月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知全集U=[-1，3]，集合A={x|lnx＜1}，B=[-1，2]，則?_U（A∩B）=（　　）

  A．[-1，0]∪（2，3]

  B．[-1，0]∪[e,3]

  C．[-1，0）∪[2，3]

  D．[-1，0]∪（2，e]
  組卷：99引用：3難度：0.7

  解析

• 2．已知復數z滿足（1-i）²z=2+2i,則z?

  z

  =（　　）

  A．2

  B．0

  C．-1+i

  D．2i
  組卷：179引用：4難度：0.8

  解析

• 3．已知

  x

  =

  e

  2

  是函數f（x）=xln（2x）-ax的極值點，則實數a的值為（　　）

  A．1

  B． e 2

  C．2

  D．e
  組卷：194引用：1難度：0.6

  解析

• 4．已知

  2

  tanθ

  +

  3

  =

  sin

  2

  θ

  1

  +

  cos

  2

  θ

  ，則tanθ=（　　）

  A．-4

  B．-3

  C． - 4 3

  D． - 1 3
  組卷：255引用：1難度：0.7

  解析

• 5．某市政府部門為了解該市的“全國文明城市”創建情況，在該市的12個區縣市中隨機抽查到了甲、乙兩縣，考核組對他們的創建工作進行量化考核．在兩個縣的量化考核成績（均為整數）中各隨機抽取20個，得到如圖數據（用頻率分布直方圖估計總體平均數時，每個區間的值均取該區間的中點值）．關于甲乙兩縣的考核成績，下列結論正確的是（　　）
  

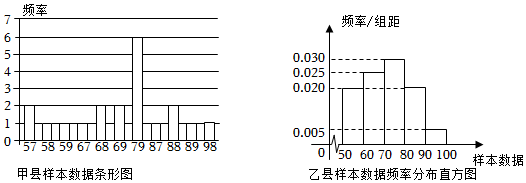
  A．甲縣平均數小于乙縣平均數

  B．甲縣中位數小于乙縣中位數

  C．甲縣眾數不小于乙縣眾數

  D．不低于80的數據個數，甲縣多于乙縣
  組卷：412引用：4難度：0.5

  解析

• 6．已知F₁，F₂是雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的兩個焦點，C的離心率為5，點P（x₀，y₀）在C上，

  P

  F

  1

  ?

  P

  F

  2

  ＜

  0

  ，則x₀的取值范圍是（　　）

  A．（-3a,3a）	B．（-3a,-a]∪[a,3a）
  C． （ - 7 5 a , 7 5 a ）	D．（- 7 5 a,-a]∪[a, 7 5 a ）
  組卷：157引用：4難度：0.8

  解析

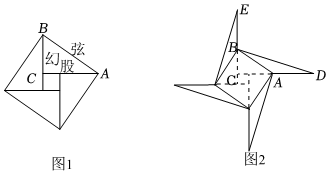• 7．勾股定理被稱為幾何學的基石，相傳在商代由商高發現，又稱商高定理．漢代數學家趙爽利用弦圖（又稱趙爽弦圖，它由四個全等的直角三角形和一個小正方形組成，如圖1），證明了商高結論的正確性．現將弦圖中的四條股延長相同的長度（如將CA延長至D）得到圖2．在圖2中，若AD=5，BD=

  3

  10

  ，D，E兩點間的距離為

  145

  ，則弦圖中小正方形的邊長為（　　）

  A． 3 2

  B． 2 2 3

  C．1

  D．2
  組卷：155引用：9難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．已知f（x）=ke^x-

  1

  2

  x

  2

  ．
  （1）若函數f（x）有兩個極值點，求實數k的取值范圍；
  （2）證明：當n∈N^*時，

  1

  2

  2

  +

  2

  3

  2

  e

  +

  3

  4

  2

  e

  2

  +…+

  n

  （

  n

  +

  1

  ）

  2

  e

  n

  -

  1

  ＜1．
  組卷：396引用：4難度：0.1

  解析

• 22．已知拋物線C：y²=2px（p＞0）的焦點為F，M（4，y₀）是拋物線C上的點，O為坐標原點，

  cos

  ∠

  OFM

  =

  -

  3

  5

  ．
  （1）求拋物線C的方程；
  （2）P（a,b）（a≠0）為拋物線C上一點，過點P的直線l與圓（x-3）²+y²=1相切，這樣的直線l有兩條，它們分別交該拋物線C于A，B（異于點P）兩點．若直線l的方程為x=ty-tb+a,當|PA|=|PB|時，求實數a的值．
  組卷：152引用：3難度：0.2

  解析