2022-2023學年浙江省杭州二中高三（上）月考數學試卷（9月份）

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x∈Z|-2≤x≤2}，B={x|log₂（x+1）≤1}，則A∩B=（　　）

  A．（-1，1]

  B．[-2，1]

  C．{0，1}

  D．{-2，-1，0，1}
  組卷：12引用：2難度：0.8

  解析

• 2．設f（x）在x₀處可導，下列式子與f'（x₀）相等的是（　　）

  A． lim Δ x → 0 f （ x 0 ） - f （ x 0 + Δ x ） Δ x

  B． lim Δ x → 0 f （ x 0 + Δ x ） - f （ x 0 - Δ x ） 2 Δ x

  C． lim Δ x → 0 f （ x 0 + 2 Δ x ） - f （ x 0 ） Δ x

  D． lim Δ x → 0 f （ x 0 ） - f （ x 0 - Δ x ） - Δ x
  組卷：383引用：3難度：0.7

  解析

• 3．a₁、b₁、c₁、a₂、b₂、c₂均為非零實數，不等式a₁x²+b₁x+c₁＞0和a₂x²+b₂x+c₂＞0的解集分別為集合M和N，那么“

  a

  1

  a

  2

  =

  b

  1

  b

  2

  =

  c

  1

  c

  2

  ”是“M=N”的（　　）

  A．充分非必要條件	B．必要非充分條件
  C．充要條件	D．既非充分又非必要條件
  組卷：321引用：9難度：0.9

  解析

• 4．2018年9月24日，阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想，這一事件引起了數學界的震動．在1859年，德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題，也就是著名的黎曼猜想．在此之前，著名數學家歐拉也曾研究過這個問題，并得到小于數字x的素數個數大約可以表示為

  π

  （

  x

  ）

  ≈

  x

  lnx

  的結論．若根據歐拉得出的結論，估計10000以內的素數的個數為（素數即質數，lge≈0.43429，計算結果取整數）（　　）

  A．1089

  B．1086

  C．434

  D．145
  組卷：74引用：4難度：0.8

  解析

• 5．已知a=e^0.1，

  b

  =

  ln

  1

  .

  2

  2

  +

  1

  ，

  c

  =

  1

  .

  2

  ，則它們的大小關系正確的是（　　）

  A．b＞a＞c

  B．c＞b＞a

  C．a＞c＞b

  D．a＞b＞c
  組卷：196引用：3難度：0.6

  解析

• 6．如圖，在正方形ABCD中，AB=2，點M從點A出發，沿A→B→C→D→A方向，以每秒2個單位的速度在正方形ABCD的邊上運動；點N從點B出發，沿B→C→D→A的方向，以每秒1個單位的速度在正方形ABCD的邊上運動．點M與點N同時出發，記運動時間為t（單位：秒），△AMN的面積為f（t）（規定A，M，N共線時其面積為零），則點M第一次到達點A時，y=f（t）的圖象為（　　）

  A．	B．
  C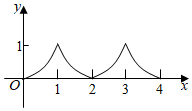．	D．
  組卷：138引用：8難度：0.8

  解析

• 7．已知函數f（x）=x（lnx-a），g（x）=

  x

  -

  a

  e

  x

  ，若對任意的x∈[1，e]，均存在x₂∈[-1，1]，使得f（x₁）=g（x₂），則a的取值可能是（　　）

  A．0

  B．2

  C．-3

  D．1
  組卷：88引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知函數f（x）=e^x，x∈R．
  （1）設m＞n,證明：

  f

  （

  m

  +

  n

  2

  ）

  ＜

  f

  （

  m

  ）

  -

  f

  （

  n

  ）

  m

  -

  n

  ；
  （2）已知f（x）=g（x）+h（x），其中g（x）為偶函數，h（x）為奇函數．若y=h（x）+b+

  c

  x

  （b,c∈R，c≠0）有兩個不同的零點x₁，x₂，證明：|x₁-x₂|＜

  b

  2

  -

  4

  c

  ．
  組卷：45引用：1難度：0.3

  解析

• 22．已知函數f（x）=asinx-ln（1+x）（a∈R）在區間（-1，0）內存在極值點．
  （1）求a的取值范圍；
  （2）判斷關于x的方程f（x）=0在（-1，π）內實數解的個數，并說明理由．
  組卷：88引用：3難度：0.4

  解析