2018-2019學年湖北省黃岡市九年級（下）開學數學試卷

一、選擇題（下列各題的備選答案中，有且僅有一個答案是正確的，每小題3分，共24分）

• 1．在如圖所示的花壇的圖案中，圓形的內部有菊花組成的內接等邊三角形，則這個圖案（　　）

  A．是軸對稱圖形但不是中心對稱圖形

  B．既是軸對稱圖形又是中心對稱圖形

  C．是中心對稱圖形但不是軸對稱圖形

  D．既不是軸對稱圖形又不是中心對稱圖形
  組卷：25引用：2難度：0.9

  解析

• 2．下列事件中發生的可能性為0的是（　　）

  A．拋一枚均勻硬幣，落地后正面朝上

  B．今天黃岡市最高氣溫為 88℃

  C．路邊拋擲一石頭，石頭終將落地（空中無任何遮攔）

  D．不透明袋子中放了大小相同的乒乓球和金屬球，從中去摸取出乒乓球
  組卷：380引用：3難度：0.8

  解析

• 3．對于拋物線y=（x-1）²+2的說法錯誤的是（　　）

  A．拋物線的開口向上

  B．拋物線的頂點坐標是（1，2）

  C．拋物線與x軸無交點

  D．當x＜1時，y隨x的增大而增大
  組卷：417引用：3難度：0.7

  解析

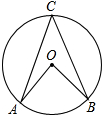• 4．OA，OB是⊙O的兩條半徑，且∠C=40°，點C在⊙O上，則∠AOB的度數為（　　）

  A．80°

  B．40°

  C．50°

  D．20°
  組卷：35引用：3難度：0.9

  解析

• 5．某廠一月份生產產品50臺，計劃二、三月份共生產產品120臺，設二、三月份平均每月增長率為x,根據題意，可列出方程為（　　）

  A．50（1+x）2=60

  B．50（1+x）2=120

  C．50+50（1+x）+50（1+x）2=120

  D．50（1+x）+50（1+x）2=120
  組卷：2684引用：25難度：0.9

  解析

• 6．已知拋物線y=（m-1）x²+4x-3（m為常數）與x軸有兩個交點，則m的取值范圍是（　　）

  A．m ＞ - 1 3	B．m＜ - 1 3
  C．m ≥ - 1 3	D．m ＞ - 1 3 ，且m≠1
  組卷：112引用：2難度：0.9

  解析

• 7．一個扇形的弧長是10πcm,面積是60πcm²，則此扇形的圓心角的度數是（　　）

  A．300°

  B．150°

  C．120°

  D．75°
  組卷：1833引用：18難度：0.7

  解析

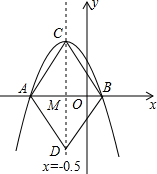• 8．如圖所示，拋物線y=ax²+bx+c（a≠0）與x軸交于點A（-2，0）、B（1，0），直線x=-0.5與此拋物線交于點C，與x軸交于點M，在直線上取點D，使MD=MC，連接AC、BC、AD、BD，某同學根據圖象寫出下列結論：
  ①a-b=0；
  ②當-2＜x＜1時，y＞0；
  ③四邊形ACBD是菱形；
  ④9a-3b+c＞0
  你認為其中正確的是（　　）

  A．②③④

  B．①②④

  C．①③④

  D．①②③
  組卷：3602引用：14難度：0.7

  解析

三、解答題（共9小題，共72分）

• 24．某保健品廠每天生產A，B兩種品牌的保健品共600瓶，A，B兩種產品每瓶的成本和利潤如表，設每天生產A產品x瓶，生產這兩種產品每天共獲利y元．
  （1）請求出y關于x的函數關系式；
  （2）如果該廠每天至少投入成本26 400元，那么每天至少獲利多少元？
  （3）該廠每天生產的A，B兩種產品被某經銷商全部訂購，廠家對A產品進行讓利，每瓶利潤降低

  x

  100

  元，廠家如何生產可使每天獲利最大？最大利潤是多少？
  

  	A	B
  成本（元/瓶）	50	35
  利潤（元/瓶）	20	15
  組卷：82引用：2難度：0.3

  解析

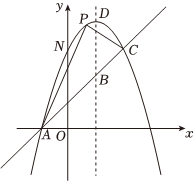• 25．如圖，已知拋物線y=-x²+bx+c與一直線相交于A（-1，0），C（2，3）兩點，與y軸交于點N．其頂點為D．
  （1）拋物線及直線AC的函數關系式；
  （2）若拋物線的對稱軸與直線AC相交于點B，E為直線AC上的任意一點，過點E作EF∥BD交拋物線于點F，以B，D，E，F為頂點的四邊形能否為平行四邊形？若能，求點E的坐標；若不能，請說明理由；
  （3）若P是拋物線上位于直線AC上方的一個動點，求△APC的面積的最大值．
  組卷：4046引用：10難度：0.5

  解析