2022-2023學年廣東省廣州六中珠江中學八年級（上）期中數學試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．計算2022⁰的結果是（　　）

  A．1

  B．0

  C．2022

  D． 1 2022
  組卷：232引用：4難度：0.9

  解析

• 2．下列圖形不具有穩定性的是（　　）

  A．直角三角形

  B．等腰三角形

  C．正方形

  D．鈍角三角形
  組卷：167引用：21難度：0.9

  解析

• 3．如圖，△ABC≌△BAD，如果AB=6cm,BD=4cm,AD=5cm,那么BC的長是（　　）

  A．4cm

  B．5cm

  C．6cm

  D．無法確定
  組卷：306引用：19難度：0.9

  解析

• 4．下列計算正確的是（　　）

  A．b3?b3=2b3	B．（-2a）2=4a2
  C．（a+b）2=a2+b2	D．（x+2）（x-2）=x2-2
  組卷：167引用：9難度：0.8

  解析

• 5．已知等腰三角形一邊長等于4，一邊長等于9，它的周長是（　　）

  A．17或22

  B．22

  C．17

  D．13
  組卷：1517引用：20難度：0.7

  解析

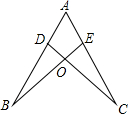• 6．如圖，點D，E分別在線段AB，AC上，CD與BE相交于O點，已知AB=AC，現添加以下的哪個條件仍不能判定△ABE≌△ACD（　　）

  A．∠B=∠C

  B．BE=CD

  C．BD=CE

  D．AD=AE
  組卷：5107引用：65難度：0.7

  解析

• 7．若一個多邊形的內角和等于720°，則這個多邊形的邊數是（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：916引用：99難度：0.9

  解析

• 8．已知a+b=3，則a²-b²+6b的值為（　　）

  A．6

  B．9

  C．12

  D．15
  組卷：246引用：9難度：0.9

  解析

三、解答題（共72分）

• 24．對任意一個數m,如果m等于兩個正整數的平方和，那么稱這個數m為“平方和數”，若m=a²+b²（a、b為正整數），記A（m）=ab.例如：29=2²+5²，29就是一個“平方和數”，則A（29）=2×5=10．
  （1）判斷45是否是“平方和數”，若是，請計算A（45）的值；若不是，請說明理由；
  （2）若k是一個不超過50的“平方和數”，且A（k）=

  k

  -

  9

  2

  ，求k的值；
  （3）對任意一個數m,如果m等于兩個整數的平方和，那么稱這個數m為“廣義平方和數”，若m和n都是“廣義平方和數”，請說明它們的乘積mn也是“廣義平方和數”．
  組卷：92引用：2難度：0.6

  解析

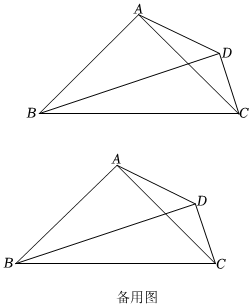• 25．如圖，四邊形ABCD中，已知∠BAC=∠BDC=90°，且AB=AC．
  （1）求證：∠ABD=∠ACD；
  （2）記△ABD的面積為S₁，△ACD的面積為S₂．
  ①求證：S₁-S₂=

  1

  2

  AD²；
  ②過點B作BC的垂線，過點A作BC的平行線，兩直線相交于M，延長BD至P，使得DP=CD，連接MP．當MP取得最大值時，求∠CBD的大小．
  組卷：308引用：4難度：0.1

  解析