當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省廣州市育才中學高二（上）期中數學試卷

發布：2024/10/5 1:0:1

一、單項選擇題：（每小題5分，共40分）

1．已知直線x+my-3=0的傾斜角為150°，則實數m的值為（　　）
A．
-
3
B．
-
3
3
C．
3
D．
3
3
組卷：31引用：1難度：0.8
解析
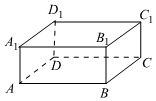2．如圖，在長方體ABCD-A₁B₁C₁D₁中，化簡
AB
-
AD
+
C
C
1
=（　　）
A．
D
B
1
B．
B
D
1
C．
A
C
1
D．
A
1
C
組卷：136引用：8難度：0.9
解析
3．方程
（
x
-
4
）
2
+
y
2
+
（
x
+
4
）
2
+
y
2
=10的化簡結果是（　　）
A．
x
2
5
+
y
2
3
=1 B．
x
2
3
+
y
2
5
=1 C．
x
2
25
+
y
2
9
=1 D．
x
2
9
+
y
2
25
=1
組卷：460引用：15難度：0.7
解析
4．一條光線從點P（5，8）射出，與x軸相交于點Q（-1，0），則反射光線所在直線在y軸上的截距為（　　）
A．
-
3
4
B．
3
4
C．
-
4
3
D．
4
3
組卷：113引用：6難度：0.8
解析
5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，
O
為橢圓的對稱中心，F為橢圓的一個焦點，P為橢圓上一點，PF⊥x軸，PF與橢圓的另一個交點為點Q，△POQ為等腰直角三角形，則橢圓的離心率為（　　）
A．
3
2
B．
5
-
1
2
C．
3
+
1
4
D．
3
5
組卷：116引用：9難度：0.5
解析
6．已知向量
OA
=
（
0
，
1
，
2
）
，
OB
=
（
-
1
，
0
，
1
）
，
OC
=
（
2
，
1
，
λ
）
，若O，A，B，C共面，則
OC
在
OB
上的投影向量的模為（　　）
A．
2
2
B．
2
C．
2
5
5
D．
5
5
組卷：325引用：10難度：0.7
解析
7．德國數學家米勒曾提出過如下的“最大視角定理”（也稱“米勒定理”）：若點A，B是∠MON的OM邊上的兩個定點，C是ON邊上的一個動點，當且僅當△ABC的外接圓與邊ON相切于點C時，∠ACB最大．在平面直角坐標系中，已知點D（2，0），E（4，0），點F是y軸負半軸的一個動點，當∠DFE最大時，△DEF的外接圓的方程是（　　）
A．
（
x
-
3
）
2
+
（
y
+
2
2
）
2
=
9
B．
（
x
-
3
）
2
+
（
y
-
2
2
）
2
=
9
C．
（
x
+
2
2
）
2
+
（
y
-
3
）
2
=
8
D．
（
x
-
2
2
）
2
+
（
y
-
3
）
2
=
8
組卷：152引用：4難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：（共70分）

21．如圖1，已知ABFE是直角梯形，EF∥AB，∠ABF=90°，∠BAE=60°，C、D分別為BF、AE的中點，AB=5，EF=1，將直角梯形ABFE沿CD翻折，使得二面角F-DC-B的大小為60°，如圖2所示，設N為BC的中點．

（1）證明：FN⊥AD；
（2）若M為AE上一點，且
AM
AE
=
λ
，則當λ為何值時，直線BM與平面ADE所成角的正弦值為
5
7
14
．
組卷：359引用：10難度：0.4
解析
22．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的焦距為2，且經過點
P
（
1
，
3
2
）
．
（1）求橢圓C的方程；
（2）經過橢圓右焦點F且斜率為k（k≠0）的動直線l與橢圓交于A、B兩點，試問x軸上是否存在異于點F的定點T，使得直線TA和TB關于x軸對稱？若存在，求出T點坐標，若不存在，說明理由．
組卷：73引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ x - 3 ） 2 + （ y + 2 2 ） 2 = 9	B．（ x - 3 ） 2 + （ y - 2 2 ） 2 = 9
C．（ x + 2 2 ） 2 + （ y - 3 ） 2 = 8	D．（ x - 2 2 ） 2 + （ y - 3 ） 2 = 8

2023-2024學年廣東省廣州市育才中學高二（上）期中數學試卷

一、單項選擇題：（每小題5分，共40分）

1．已知直線x+my-3=0的傾斜角為150°，則實數m的值為（ ）

2．如圖，在長方體ABCD-A1B1C1D1中，化簡AB-AD+CC1=（ ）

3．方程（x-4）2+y2+（x+4）2+y2=10的化簡結果是（ ）

4．一條光線從點P（5，8）射出，與x軸相交于點Q（-1，0），則反射光線所在直線在y軸上的截距為（ ）

5．已知橢圓C：x2a2+y2b2=1（a＞b＞0），O為橢圓的對稱中心，F為橢圓的一個焦點，P為橢圓上一點，PF⊥x軸，PF與橢圓的另一個交點為點Q，△POQ為等腰直角三角形，則橢圓的離心率為（ ）

6．已知向量OA=（0，1，2），OB=（-1，0，1），OC=（2，1，λ），若O，A，B，C共面，則OC在OB上的投影向量的模為（ ）

四、解答題：（共70分）

1．已知直線x+my-3=0的傾斜角為150°，則實數m的值為（　　）

2．如圖，在長方體ABCD-A₁B₁C₁D₁中，化簡
AB
-
AD
+
C
C
1
=（　　）

3．方程
（
x
-
4
）
2
+
y
2
+
（
x
+
4
）
2
+
y
2
=10的化簡結果是（　　）

4．一條光線從點P（5，8）射出，與x軸相交于點Q（-1，0），則反射光線所在直線在y軸上的截距為（　　）

5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，
O
為橢圓的對稱中心，F為橢圓的一個焦點，P為橢圓上一點，PF⊥x軸，PF與橢圓的另一個交點為點Q，△POQ為等腰直角三角形，則橢圓的離心率為（　　）

6．已知向量
OA
=
（
0
，
1
，
2
）
，
OB
=
（
-
1
，
0
，
1
）
，
OC
=
（
2
，
1
，
λ
）
，若O，A，B，C共面，則
OC
在
OB
上的投影向量的模為（　　）