2023年陜西省咸陽市武功縣普集高級中學高考數學模考試卷(文科)(5月份)(三)
發布:2024/8/27 1:0:9
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知集合A={x|
<1},B={x|x2-2x-8>0},則A∩B=( )1xA.{x|x<-2或x>4} B.{x|x>4} C.{x|-2<x<0或1<x<4} D.{x|1<x<4} 組卷:140引用:2難度:0.8 -
2.已知(1+i)2z=3+2i,則|z|=( )
A. 134B.3 C. 132D. 133組卷:186引用:5難度:0.8 -
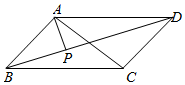 3.如圖,在平行四邊形ABCD中,AP⊥BD,垂足為P,且AP=4,則=( )AP?AC
3.如圖,在平行四邊形ABCD中,AP⊥BD,垂足為P,且AP=4,則=( )AP?ACA.32 B.18 C.16 D.8 組卷:365引用:3難度:0.7 -
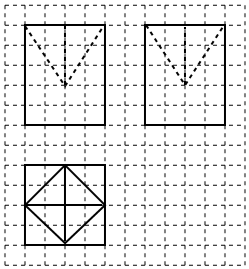 4.如圖,網格紙中小正方形的邊長為1,粗線畫出的是某幾何體的三視圖,則該幾何體的體積為( )
4.如圖,網格紙中小正方形的邊長為1,粗線畫出的是某幾何體的三視圖,則該幾何體的體積為( )A.72 B.64 C.56 D.32 組卷:160引用:5難度:0.6 -
5.如圖是國家統計局2021年11月發布的全國居民消費價格的漲跌幅情況,現有如下說法:
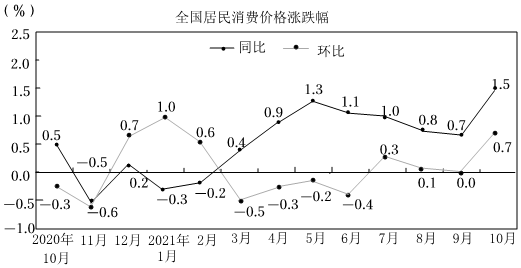
①2021年10月份,全國居民消費價格的同比和環比均呈現增漲趨勢;
②2020年10月至2021年10月,全國居民消費價格同比增漲的月份個數是下跌的5倍;
③從2020年10月至2021年10月中任取1個月,全國居民消費價格的同比呈現增漲的概率為;1013
則上述說法正確的個數為( )A.0 B.1 C.2 D.3 組卷:30引用:6難度:0.8 -
6.若數列{an}滿足a1=-3,an+1=
,則a2022的值為( )1+an1-anA.2 B.-3 C. -12D. 13組卷:174引用:3難度:0.7 -
7.如果一個凸多面體的每個面都是全等的正多邊形,而且每個頂點都引出相同數目的棱,那么這個凸多面體叫做正多面體.古希臘數學家歐幾里得在其著作《幾何原本》的卷13中系統地研究了正多面體的作圖,并證明了每個正多面體都有外接球.若正四面體、正方體、正八面體的外接球半徑相同,則它們的棱長之比為( )
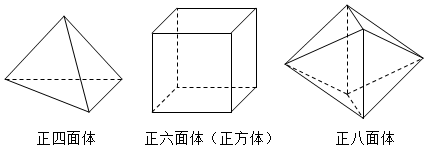
A. 2:1:3B. 2:2:3C. 2:2:1D. 2:2:3組卷:365引用:3難度:0.6
選考題:共10分.請考生在第22、23題中任選一題作答,如果多做,則按所做的第一題計分.[選修4-4:極坐標系與參數方程]
-
22.在直角坐標系xOy中,直線l的參數方程為
(t∈R,t為參數,α∈(0,x=tcosαy=-2+tsinα)).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,半圓C的極坐標方程為π2.ρ=2sinθ,θ∈(π4,3π4)
(1)求半圓C的參數方程和直線l的直角坐標方程;
(2)直線l與x軸交于點A,與y軸交于點B,點D在半圓C上,且直線CD的傾斜角是直線l的傾斜角的2倍,△ABD的面積為1+,求α的值.3組卷:153引用:9難度:0.7 -
23.已知函數f(x)=|x-
|+|x+b+c|(a,b,c均為正實數).a2
(1)當a=b=c=1時,求f(x)得最小值;
(2)當f(x)的最小值為3時,求a2+b2+c2的最小值.組卷:48引用:5難度:0.7


