當前位置：試卷中心 > 試卷詳情

2020-2021學年江蘇省南通市啟東中學高一（下）第二次月考數學試卷

發布：2024/11/26 11:0:2

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

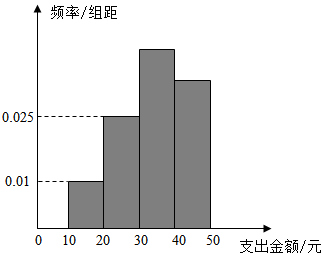1．為了解學生在課外活動方面的支出情況，抽取了n個同學進行調查，結果顯示這些學生的支出金額（單位：元）都在[10，50]，其中支出金額在[30，50]的學生有117人，頻率分布直方圖如圖所示，則n=（　　）
A．180 B．160 C．150 D．200
組卷：114引用：3難度：0.7
解析
2．已知
a
=（1，sin²x），
b
=（2，sin2x），其中x∈（0，π）．若|
a
?
b
|=|
a
|?|
b
|，則tanx的值等于（　　）
A．1 B．-1 C．
3
D．
2
2
組卷：103引用：8難度：0.9
解析
3．已知
α
∈
R
，
sinα
+
2
cosα
=
10
2
，則tan2α=（　　）
A．
4
3
B．
3
4
C．
-
3
4
D．
-
4
3
組卷：2359引用：56難度：0.9
解析
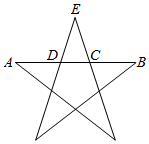4．黃金分割點是指將一條線段分為兩部分，使得較長部分與整體線段的長的比值為
5
-
1
2
的點．利用線段上的兩個黃金分割點可以作出正五角星，如圖所示，已知C，D為AB的兩個黃金分割點，研究發現如下規律：
AC
AB
=
BD
AB
=
CD
BC
=
5
-
1
2
．若△CDE是頂角為36°的等腰三角形，則cos216°=（　　）
A．
-
5
+
1
4
B．
-
5
-
1
4
C．
-
5
+
1
2
D．
-
5
-
1
2
組卷：240引用：3難度：0.5
解析
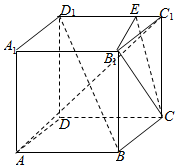5．如圖，E是正方體ABCD-A₁B₁C₁D₁的棱C₁D₁上的一點E（不與端點重合），BD₁∥平面B₁CE，則（　　）
A．BD₁∥CE B．AC₁⊥BD₁ C．D₁E=2EC₁ D．D₁E=EC₁
組卷：1122引用：10難度：0.7
解析
6．非零向量
a
，
b
滿足：|
a
-
b
|=|
a
|，
a
?
（
a
-
b
）
=
0
，則
a
-
b
與
b
夾角的大小為（　　）
A．135° B．120° C．60° D．45°
組卷：545引用：14難度：0.7
解析
7．△ABC的內角A，B，C的對邊分別為a,b,c,且（2b-c）cosA=acosC，b=2
3
，若邊BC的中線等于3，則△ABC的面積為（　　）
A．9
3
B．
9
3
2
C．3
3
D．
3
3
2
組卷：831引用：6難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

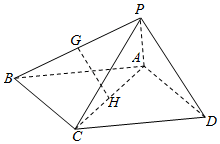21．如圖，在四棱錐P-ABCD中，底面ABCD為平行四邊形，△PCD為等邊三角形，平面PAC⊥平面PCD，PA⊥CD，CD=2，AD=3．
（Ⅰ）設G，H分別為PB，AC的中點，求證：GH∥平面PAD；
（Ⅱ）求證：PA⊥平面PCD；
（Ⅲ）求直線AD與平面PAC所成角的正弦值．
組卷：5534引用：27難度：0.4
解析
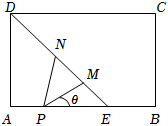22．如圖所示，矩形ABCD是一個歷史文物展覽廳的俯視圖，點E在AB上，在梯形BCDE區域內部展示文物，DE是玻璃幕墻，游客只能在△ADE區域內參觀，在AE上點P處安裝一可旋轉的監控攝像頭，∠MPN為監控角，其中M，N在線段DE（含端點）上，且點M在點N的右下方，經測量得知，AD=6m,AE=6m,AP=2m,
∠
MPN
=
π
4
．記∠EPM=θ（rad），監控攝像頭的可視區域△PMN的面積為Sm²．
（1）求S關于θ的函數關系式，并寫出θ的取值范圍；（參考數據：
tan
5
4
≈
3
）
（2）求S的最小值．
組卷：34引用：2難度：0.5
解析