2022-2023學年河南省新鄉市長垣市高二（下）第三次聯考數學試卷
發布：2024/7/9 8:0:8
一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．
-
1．某外語組有9人，其中5人會英語，4人會日語，從中選出會英語和日語的各一人，不同的選法有（ ）
組卷：725引用：2難度：0.8 -
2．兩個變量y與x的回歸模型中，分別選擇了4個不同的模型，其中擬合效果最好的模型是（ ）
組卷：70引用：2難度：0.7 -
3．現有4道填空題，學生張三對其中3道題有思路，1道題思路不清晰．有思路的題做對的概率為
，思路不清晰的題做對的概率為34，張三從這4道填空題中隨機選擇1題，則他做對該題的概率為（ ）14組卷：40引用：4難度：0.7 -
4．小明收集了五枚不同的銅錢，準備將其串成精美的掛件（如圖），根據不同的排放順序，不同的串法有（ ）組卷：16引用：4難度：0.7 -
5．已知定義在區間（a,b）上的函數f（x）的導函數為f′（x），f′（x）的圖象如圖所示，則（ ）組卷：53引用：6難度：0.5 -
6．已知由樣本數據（xi，yi）（i=1，2，3，…，10）組成的一個樣本，得到回歸直線方程為
，且?y=2x-0.4，去除兩個樣本點（-3，1）和（3，-1）后，新得到的回歸直線方程斜率為3，則樣本（4，8）的殘差為（ ）x=2組卷：64引用：4難度：0.7 -
7．流感病毒分為甲、乙、丙三型，甲型流感病毒最容易發生變異，流感大流行就是甲型流感病毒出現新亞型或舊亞型重現引起的．根據以往的臨床記錄，某種診斷甲型流感病毒的試驗具有如下的效果：若以A表示事件“試驗反應為陽性”，以C表示事件“被診斷者患有甲型流感”，則有P（A|C）=0.9，
．現對自然人群進行普查，設被試驗的人患有甲型流感的概率為0.005，即P（C）=0.005，則P（C|A）=（ ）P（A|C）=0.9組卷：108引用：4難度：0.7
四、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．
-
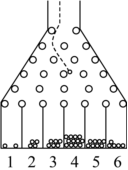21．高爾頓板又稱豆機、梅花機等，是英國生物統計學家高爾頓設計用來研究隨機現象的模型．如圖所示的高爾頓板為一塊木板自上而下釘著6層圓柱形小木塊，最頂層有2個小木塊，以下各層小木塊的個數依次遞增，各層小木塊互相平行但相互錯開，小木塊之間留有適當的空隙作為通道，前面擋有一塊透明玻璃．讓小球從高爾頓板上方的通道口落下，小球在下落過程中與層層小木塊碰撞，且等可能向左或者向右滾下，最后落入高爾頓板下方從左至右編號為1，2，…，6的球槽內．
（1）某商店將該高爾頓板改良成游戲機，針對某商品推出促銷活動．凡是入店購買該商品一件，就可以獲得一次游戲機會．若小球落入X號球槽，該商品可立減Y元，其中Y=|20-5X|．若該商品的成本價是10元，從期望的角度考慮，為保證該商品總體能盈利，求該商品的最低定價．（結果取整數）
（2）將79個小球依次從高爾頓板上方的通道口落下，試問3號球槽中落入多少個小球的概率最大？
附：設隨機變量ξ～B（n,p），則ξ的分布列為，k=0，1，2，?，n.P（ξ=k）=Cknpk（1-p）n-k．P（ξ=k）P（ξ=k-1）=Cknpk（1-p）n-kCk-1npk-1（1-p）n-k+1=1+（n+1）p-kk（1-p）組卷：146引用：5難度：0.5 -
22．已知函數f（x）=ln（x+1）．
（1）求函數的最大值；g（x）=f（x）-x4-1
（2）證明：當x＞0時，．f（x）＜ex-1x2
（參考數據：ln2≈0.69）組卷：40引用：6難度：0.3