2022-2023學年江西省南昌市南昌縣蓮塘一中高二（上）月考數學試卷（10月份）

一、選擇題(本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一個是符合題目要求的。)

• 1．下列有關直線l：x+my-1=0（m∈R）的說法中正確的是（　　）

  A．直線l的斜率為-m	B．直線l的斜率為 - 1 m
  C．直線l過定點（0，1）	D．直線l過定點（1，0）
  組卷：204引用：4難度：0.7

  解析

• 2．若方程

  x

  2

  m

  -

  5

  +

  y

  2

  m

  +

  4

  =

  1

  表示的圖形是雙曲線，則m的取值范圍是（　　）

  A．m＞5

  B．m＜-4

  C．m＜-4或m＞5

  D．-4＜m＜5
  組卷：56引用：3難度：0.7

  解析

• 3．已知圓（x+1）²+（y+2）²=4關于直線ax+by+1=0（a＞0，b＞0）對稱，則

  1

  a

  +

  2

  b

  的最小值為（　　）

  A． 5 2

  B．9

  C．4

  D．8
  組卷：839引用：12難度：0.8

  解析

• 4．古希臘數學家阿基米德利用“逼近法”得到橢圓的面積除以圓周率等于橢圓的長半軸長與短半軸長的乘積．若橢圓C的中心為原點，焦點F₁，F₂均在x軸上，C的面積為

  2

  3

  π

  ，且短軸長為

  2

  3

  ，則C的標準方程為（　　）

  A． x 2 12 + y 2 = 1

  B． x 2 4 + y 2 3 = 1

  C． x 2 3 + y 2 4 = 1

  D． x 2 16 + y 2 3 = 1
  組卷：271引用：8難度：0.8

  解析

• 5．已知動圓圓心在拋物線x²=4y上，且動圓恒與直線y=-1相切，則此動圓必過定點（　　）

  A．（2，0）

  B．（1，0）

  C．（0，1）

  D．（0，-1）
  組卷：94引用：2難度：0.7

  解析

• 6．已知圓O₁：x²+y²-2x-3=0與圓O₂：x²+y²-4x+2y+3=0相交于點A，B，則四邊形AO₁BO₂的面積是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：267引用：3難度：0.6

  解析

• 7．點A（0，-1）到直線kx-y+k=0距離的最大值為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：318引用：2難度：0.5

  解析

四、解答題（本大題共6小題，共70分，解答應寫出文字說明，證明過程或演算步驟。）

• 21．在①過點C（2，0），②圓E恒被直線mx-y-m=0（m∈R）平分，③與y軸相切，這三個條件中任選一個，補充在下面問題中，并解答．
  已知圓E經過點A（0，0），B（1，1），_____．
  （1）求圓E的一般方程；
  （2）設P是圓E上的動點，求線段AP的中點M的軌跡方程．
  組卷：154引用：11難度：0.6

  解析

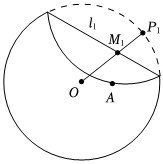• 22．用圓規畫一個圓O，然后在圓內標記點A，并把圓周上的點P₁折疊到點A，連接OP₁，標記出OP₁與折痕l₁的交點M₁（如圖），若不斷在圓周上取新的點P₂，P₃，…．進行折疊并得到標記點M₂，M₃，…．
  設圓O的半徑為4，點A到圓心O的距離為2，所有的點M₁，M₂，M₃，…形成的軌跡記為曲線C．
  （1）以OA所在的直線為x軸，OA的中垂線為y軸建立平面直角坐標系，求曲線C的標準方程；
  （2）設直線l：y=

  6

  x+m與曲線C交于E，F兩點，且以EF直徑的圓經過曲線C的中心，求實數m的值．
  組卷：53引用：3難度：0.5

  解析