2022-2023學年黑龍江省哈爾濱一中高一（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知i是虛數單位，復數z=

  2

  i

  1

  -

  i

  ，則復數z的虛部為（　　）

  A．i

  B．-i

  C．1

  D．-1
  組卷：137引用：6難度：0.8

  解析

• 2．已知a,b,c為三條不同的直線，α，β，γ為三個不同的平面，則下列說法正確的是（　　）

  A．若a∥b,b?α，則a∥α

  B．若a?α，b?β，a∥b,則α∥β

  C．若α∥β，a∥α，則a∥β

  D．若α∩β=a,β∩γ=b,α∩γ=c,a∥b,則b∥c
  組卷：514引用：11難度：0.7

  解析

• 3．若平面向量

  a

  與

  b

  的夾角為60°，

  a

  =

  （

  2

  ，

  0

  ）

  ，

  |

  b

  |

  =

  1

  ，則

  |

  a

  +

  2

  b

  |

  等于（　　）

  A． 3

  B． 2 3

  C．4

  D．12
  組卷：1323引用：24難度：0.7

  解析

• 4．已知向量

  a

  =（cosα，3），

  b

  =（sinα，-4），

  a

  ∥

  b

  ，則

  3

  sinα

  +

  cosα

  2

  cosα

  -

  3

  sinα

  的值是（　　）

  A．- 1 2

  B．-2

  C．- 4 3

  D． 1 2
  組卷：537引用：7難度：0.8

  解析

• 5．已矨A，B，C均在球O的球面上運動，且滿足

  ∠

  AOB

  =

  π

  3

  ，若三棱錐O-ABC體積的最大值為6，則球O的體積為（　　）

  A．12π

  B．48π

  C． 32 3 π

  D． 64 3 π
  組卷：43引用：2難度：0.6

  解析

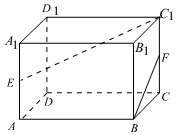• 6．如圖，在長方體ABCD-A₁B₁C₁D₁中，AA₁=AD=2，AB=3，E，F分別為棱AA₁，CC₁的中點，過BF的平面α與直線C₁E平行，則平面α截該長方體所得截面的面積為（　　）

  A．3

  B． 3 2

  C． 3 3

  D． 3 5
  組卷：565引用：3難度：0.6

  解析

• 7．圣?索菲亞教堂（英語：SAINT SOPHIA CATHEDRAL）坐落于中國黑龍江省，是一座始建于1907年拜占庭風格的東正教教堂，距今已有114年的歷史，為哈爾濱的標志性建筑.1996年經國務院批準，被列為第四批全國重點文物保護單位，是每一位到哈爾濱旅游的游客拍照打卡的必到景點．其中央主體建筑集球，圓柱，棱柱于一體，極具對稱之美，可以讓游客從任何角度都能領略它的美．小明同學為了估算索菲亞教堂的高度，在索菲亞教堂的正東方向找到一座建筑物AB，高為（

  15

  3

  -

  15

  ）m,在它們之間的地面上的點M（B，M，D三點共線）處測得樓頂A，教堂頂C的仰角分別是15°和60°，在樓頂A處測得塔頂C的仰角為30°，則小明估算索菲亞教堂的高度為（　　）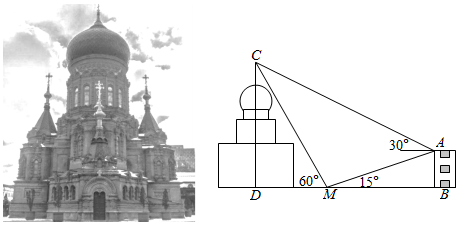
  

  A．20m

  B．30m

  C． 20 3 m

  D． 30 3 m
  組卷：360引用：21難度：0.7

  解析

三、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．某公園有一塊三角形空地，如圖，在△ABC中，

  AB

  =

  AC

  =

  100

  3

  ，∠BAC=120°，為了增加公園的觀賞性，公園管理人員擬在△ABC中間挖出一個池塘AEF用來放養觀賞魚，E，F在邊BC上，且∠EAF=60°．
  （1）若BE=100，求EF的長；
  （2）為節省投入資金，池塘△AEF的面積需要盡可能的小，記∠EAB=θ，試確定θ為何值時，池塘的面積最小．
  組卷：69引用：4難度：0.6

  解析

• 22．在銳角△ABC中，角A，B，C所對的邊分別為a,b,c,若ccosB+bcosC=2acosA．
  （1）求角A的大小；
  （2）求

  1

  tan

  B

  +

  1

  tan

  C

  的取值范圍．
  組卷：44引用：2難度：0.5

  解析