2022-2023學年福建省福州十八中高二（下）期中數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．直線

  x

  +

  3

  y

  -

  1

  =

  0

  的傾斜角為（　　）

  A． π 3

  B． π 6

  C． 2 π 3

  D． 5 π 6
  組卷：337引用：44難度：0.9

  解析

• 2．已知直線l₁：mx-y+1=0，l₂：2x-（m-1）y+1=0（m∈R），則下列結論正確的是（　　）

  A．直線l1過定點（0，-1）

  B．當l1⊥l2時， m = 1 3

  C．當l1∥l2時，m=2

  D．當l1∥l2時，兩直線l1、l2之間的距離為 2 4
  組卷：171引用：1難度：0.7

  解析

• 3．已知S_n是等比數列{a_n}的前n項和，若存在m∈N^*，滿足

  S

  2

  m

  S

  m

  =

  9

  ，

  a

  2

  m

  a

  m

  =

  5

  m

  +

  1

  m

  -

  1

  ，則數列{a_n}的公比為（　　）

  A．-2

  B．2

  C．-3

  D．3
  組卷：159引用：5難度：0.8

  解析

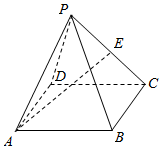• 4．四棱錐P-ABCD中，底面ABCD是平行四邊形，點E為棱PC的中點，若

  AE

  =x

  AB

  +2y

  BC

  +3z

  AP

  ，則x+y+z等于（　　）

  A．1

  B． 11 12

  C． 11 6

  D．2
  組卷：797引用：12難度：0.7

  解析

• 5．從0，1，2，3，4，5，6七個數字中取四個不同的數組成被5整除的四位數，這樣的四位數的個數有（　　）

  A．260

  B．240

  C．220

  D．200
  組卷：75引用：2難度：0.7

  解析

• 6．已知函數f（x）的導函數是f′（x），若f（x）=f′（1）x³+x²-1，則下列結論正確的是（　　）

  A．f（-2）=-5

  B．f（x）在（-∞，0）∪（ 2 3 ，+∞）上單調遞減

  C．x=0為函數f（x）的極大值點

  D．曲線y=f（x）在x=1處切線為y=-x
  組卷：74引用：2難度：0.5

  解析

• 7．已知F₁，F₂是雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的左、右焦點，點F₁關于漸近線的對稱點恰好落在以F₂為圓心，|OF₂|為半徑的圓上，則該雙曲線的離心率為（　　）

  A． 2

  B． 3

  C．2

  D． 3 + 1
  組卷：21引用：3難度：0.6

  解析

四、解答題（本大題共6小題，共70分．解答時應寫出必要的文字說明證明過程或演算步驟）

• 21．已知函數f（x）=lnx-x.
  （1）求曲線y=f（x）在x=e處的切線方程；
  （2）求函數g（x）=f（x）+2x-4lnx-

  2

  x

  的單調區間和極值；
  （3）若不等式f（x）≤（a-1）x+1在（0，+∞）上恒成立，求實數a的取值范圍．
  組卷：128引用：3難度：0.6

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）過點P（2，1），F₁，F₂分別為橢圓C的左、右焦點，且|PF₁|+|PF₂|=4

  2

  ．
  （1）求橢圓C的標準方程；
  （2）點M，N是橢圓C上與點P不重合的兩點，且以MN為直徑的圓過點P，若直線MN過定點，求出該定點；若不過定點，請說明理由．
  組卷：31引用：2難度：0.5

  解析