2021-2022學年江蘇省無錫市江陰高級中學高二（上）期中數學試卷

一、單選題（本大題共8小題，共40.0分.在每小題列出的選項中，選出符合題目的一項）

• 1．直線

  3

  x-y+a=0（a∈R）的傾斜角為（　　）

  A．30°

  B．60°

  C．150°

  D．120°
  組卷：289引用：17難度：0.9

  解析

• 2．雙曲線

  x

  2

  a

  2

  -

  y

  2

  4

  =

  1

  （

  a

  ＞

  0

  ）

  的一個焦點到漸近線的距離為（　　）

  A． 2 a

  B． a 2

  C．2

  D．4
  組卷：229引用：4難度：0.7

  解析

• 3．若橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）滿足2b=a+c,則該橢圓的離心率e=（　　）

  A． 5 5

  B． 10 4

  C． 3 5

  D． 1 + 5 2
  組卷：778引用：7難度：0.8

  解析

• 4．若橢圓

  x

  2

  m

  +

  y

  2

  n

  =1（m＞n＞0）和雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞b＞0）有相同的焦點F₁、F₂，P是兩條曲線的一個交點，則|PF₁|?|PF₂|的值是（　　）

  A．m-a2

  B． 1 2 (m-a2)

  C．m2-a2

  D． m - a
  組卷：146引用：4難度：0.8

  解析

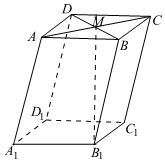• 5．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為AC與BD的交點，若|

  A

  1

  B

  1

  |=|

  A

  1

  D

  1

  |=|

  A

  1

  A

  |=2，∠AA₁D₁=90°，∠AA₁B₁=∠B₁A₁D₁=60°，則|

  B

  1

  M

  |的值為（　　）

  A．1

  B． 3

  C．2

  D． 2 3
  組卷：155引用：7難度：0.5

  解析

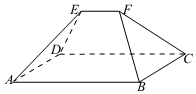• 6．《九章算術》是古代中國乃至東方的第一部自成體系的數學專著，書中記載了一種名為“芻甍”的五面體（如圖），其中四邊形ABCD為矩形，EF∥AB，若AB=3EF，△ADE和△BCF都是正三角形，且AD=2EF，則異面直線DE與BF所成角的大小為（　　）

  A． π 2

  B． π 4

  C． π 3

  D． π 6
  組卷：127引用：6難度：0.6

  解析

• 7．在平面直角坐標系xOy中，圓C的一般方程為x²+y²-6x-8y+24=0，點A，B是圓C上不同兩點，|AB|=

  6

  5

  ，點M為AB的中點，則|OM|的取值范圍為（　　）

  A．[4， 28 5 ]

  B．[ 21 5 ， 29 5 ]

  C．[4，6]

  D．[5， 31 5 ]
  組卷：92引用：2難度：0.7

  解析

四、解答題（本大題共6小題，共70.0分.解答應寫出文字說明，證明過程或演算步驟）

• 21．已知點A（8，0），點B（4，0），動點M（x,y）滿足：|MA|=

  2

  |MB|．
  （1）求點M的軌跡方程；
  （2）過點E（1，0）的直線交圓于P、Q兩點，交y軸于F點，若

  FP

  =λ₁

  PE

  ，FQ=λ₂

  QE

  ，求證：λ₁+λ₂為定值．
  組卷：71引用：3難度：0.4

  解析

• 22．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的實半軸長為1，且C上的任意一點M到C的兩條漸近線的距離乘積為

  3

  4

  ．
  （1）求雙曲線C的方程；
  （2）設直線l過雙曲線C的右焦點F，與雙曲線C相交于P，Q兩點，問在x軸上是否存在定點D，使得∠PDQ的平分線與x軸或y軸垂直？若存在，求出定點D的坐標；否則，說明理由．
  組卷：223引用：3難度：0.4

  解析