2023-2024學年北京六十六中高二（上）第一次質檢數學試卷

一、選擇題（共10小題，每小題4分，共40分）

• 1．空間向量

  OA

  -

  OB

  +

  AC

  =（　　）

  A． AB

  B． CB

  C． OC

  D． BC
  組卷：240引用：5難度：0.7

  解析

• 2．已知向量

  a

  =（8，-2，1），

  b

  =（-4，1，k），且

  a

  ∥

  b

  ，那么實數k的值為（　　）

  A． 1 2

  B． - 1 2

  C．-2

  D．2
  組卷：600引用：7難度：0.7

  解析

• 3．已知直線l經過點A（1，1，2），B（0，1，0），平面α的一個法向量為

  n

  =（-2，0，-4），則（　　）

  A．l∥α	B．l⊥α
  C．l?α	D．l與α相交，但不垂直
  組卷：573引用：9難度：0.8

  解析

• 4．經過點P（-1，0）且傾斜角為60°的直線的方程是（　　）

  A． 3 x-y-1=0

  B． 3 x - y + 3 = 0

  C． 3 x - y - 3 = 0

  D． x - 3 y + 1 = 0
  組卷：689引用：8難度：0.9

  解析

• 5．直線l₁：y=kx+b（kb≠0）和直線l₂：

  x

  k

  +

  y

  b

  =1在同一坐標系中可能是（　　）

  A．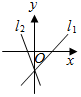

  B．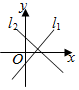

  C．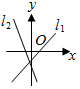

  D．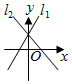
  組卷：654引用：11難度：0.7

  解析

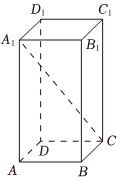• 6．已知在長方體ABCD-A₁B₁C₁D₁中，AB=AD=1，AA₁=2，那么直線A₁C與平面AA₁D₁D所成角的正弦值為（　　）

  A． 6 6

  B． 35 6

  C． 3 3

  D． 6 3
  組卷：619引用：4難度：0.6

  解析

三、解答題（共4小題；共45分）

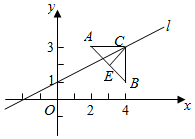• 18．如圖，已知點A（2，3），B（4，1），△ABC是以AB為底邊的等腰三角形，點C在直線l：x-2y+2=0上．
  （Ⅰ）求AB邊上的高CE所在直線的方程；
  （Ⅱ）求△ABC的面積．
  組卷：1022引用：22難度：0.5

  解析

• 19．如圖所示，在四棱柱ABCD-A₁B₁C₁D₁中，側棱A₁A⊥底面ABCD，AB⊥AC，AB=1，AC=AA₁=2，AD=CD=

  5

  ，且點M和N分別為B₁C和D₁D的中點．
  （1）求證：MN∥平面ABCD；
  （2）求點B₁到平面D₁AC的距離；
  （3）在棱A₁B₁上是否存在點E，使得直線NE和平面ABCD所成角的正弦值為

  1

  3

  ？若存在試求出點E的位置，若沒有說明理由．
  組卷：81引用：2難度：0.5

  解析