2022-2023學(xué)年遼寧省錦州市遼西育明高級中學(xué)高一（下）期中數(shù)學(xué)試卷

一、單選題：（每題5分，共40分）

• 1．在△ABC中，角A，B，C的對邊分別為a,b,c,若

  sin

  A

  =

  1

  3

  ，

  a

  =

  2

  2

  ，b=3，則sinB=（　　）

  A． 2 3

  B． 2 4

  C． 2 2

  D． 2 2 3
  組卷：47引用：2難度：0.7

  解析

• 2．cos20°cos70°-sin160°sin70°=（　　）

  A．0

  B． 1 2

  C． 3 2

  D．1
  組卷：123引用：2難度：0.9

  解析

• 3．已知平面向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  1

  ，

  3

  ）

  ，則

  a

  與

  b

  夾角的大小為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：54引用：2難度：0.8

  解析

• 4．如圖是杭州2022年第19屆亞運會會徽，名為“潮涌”，象征著新時代中國特色社會主義大潮的涌動和發(fā)展．如圖是會徽的幾何圖形，設(shè)弧AD長度是l₁，弧BC長度是l₂，幾何圖形ABCD面積為S₁，扇形BOC面積為S₂，若

  l

  1

  l

  2

  =

  2

  ，則

  S

  1

  S

  2

  =（　　）
  

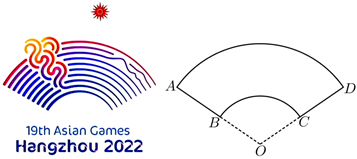
  A．1

  B．2

  C．3

  D．4
  組卷：254引用：9難度：0.7

  解析

• 5．已知α是第二象限角，則點

  P

  （

  tan

  α

  2

  ，

  sin

  2

  α

  ）

  位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：100引用：3難度：0.6

  解析

• 6．計算

  3

  tan

  80

  °

  -

  3

  tan

  50

  °

  -

  3

  tan

  80

  °

  tan

  50

  °

  的值為（　　）

  A． 3 3

  B． 3

  C． - 3 3

  D． - 3
  組卷：175引用：2難度：0.8

  解析

• 7．已知

  sin

  （

  π

  -

  α

  ）

  =

  -

  2

  sin

  （

  π

  2

  +

  α

  ）

  ，則sinαcosα等于（　　）

  A． 2 5

  B． - 2 5

  C． 1 5

  D． - 1 5
  組卷：260引用：2難度：0.7

  解析

四、解答題：（本題共六道大題，共70分，解答應(yīng)寫出文字說明，證明過程或演算步驟.）

• 21．在△ABC中，內(nèi)角A，B，C所對的邊分別為a,b,c,且

  3

  acos

  C

  =

  csin

  A

  ．
  （1）求角C的大小；
  （2）已知

  c

  =

  2

  3

  ，若△ABC為銳角三角形，求a+b的取值范圍．
  組卷：92引用：4難度：0.6

  解析

• 22．已知函數(shù)f（x）=sin²

  x

  2

  +sin

  x

  2

  cos

  x

  2

  -

  1

  2

  ．
  （1）常數(shù)ω＞0，若函數(shù)y=f（ωx）的最小正周期是π，求ω的值．
  （2）若g（x）=

  2

  f（x+

  π

  4

  ），且方程g（2x）+ag（x）-ag（

  π

  2

  -x）-a-1=0在[-

  π

  4

  ，

  π

  2

  ]上有實數(shù)解，求實數(shù)a的取值范圍．
  組卷：134引用：4難度：0.5

  解析