2022-2023學年江西省吉安市井岡山市寧岡中學高一（下）期末數學試卷

一、單選題（每題5分，共40分）

• 1．設集合A={y|y=x²+1}，則下列元素屬于A的是（　　）

  A．（0，1）

  B．-1

  C． 2

  D．0
  組卷：271引用：2難度：0.8

  解析

• 2．已知a,b∈R，則“a＞b”的一個必要條件是（　　）

  A．|a|＞|b|

  B．a2＞b2

  C．a＞b+1

  D．a＞b-1
  組卷：157引用：3難度：0.8

  解析

• 3．設函數f（x）=（a-1）x+1是R上的減函數，則有（　　）

  A．a≥1

  B．a≤1

  C．a＞1

  D．a＜1
  組卷：299引用：2難度：0.5

  解析

• 4．計算

  2

  -

  （

  1

  2

  ）

  +

  （

  -

  4

  ）

  0

  2

  +

  1

  2

  -

  1

  -

  （

  1

  -

  5

  ）

  0

  ，結果是（　　）

  A．1

  B． 2 2

  C． 2

  D． 2 - 1 2
  組卷：1219引用：11難度：0.9

  解析

• 5．函數

  y

  =

  -

  3

  sin

  （

  2

  x

  -

  π

  6

  ）

  的單調遞增區間是（　　）

  A． [ kπ + π 3 ， kπ + 5 π 6 ] ， k ∈ Z	B． [ kπ - π 6 ， kπ + π 3 ] ， k ∈ Z
  C． [ 2 kπ + π 3 ， 2 kπ + 5 π 6 ] ， k ∈ Z	D． [ 2 kπ - π 6 ， 2 kπ + π 3 ] ， k ∈ Z
  組卷：220引用：3難度：0.7

  解析

• 6．已知向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  b

  =

  （

  2

  ，

  m

  ）

  ，且

  a

  ⊥

  b

  ，則m=（　　）

  A．-6

  B．6

  C． 3 2

  D． - 3 2
  組卷：12引用：2難度：0.7

  解析

• 7．“不以規矩，不成方圓”．出自《孟子?離婁章句上》．“規”指圓規，“矩”指由相互垂直的長短兩條直尺構成的角尺，用來測量、畫圓和方形圖案的工具．有一圓形木板，以“矩”量之，較長邊為10cm,較短邊為5cm,如圖所示，將這個圓形木板截出一塊三角形木板，三角形定點A，B，C都在圓周上，角A，B，C分別對應a,b,c,滿足c=4

  5

  cm.若S_△ABC=8cm²，且a＞c,則（　　）

  A．sinC= 3 5

  B．△ABC周長為 12 + 4 5 cm

  C．△ABC周長為 15 + 4 5 cm

  D．圓形木板的半徑為 2 5 cm
  組卷：85引用：6難度：0.5

  解析

四、解答題（共70分）

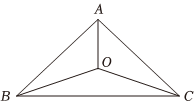• 21．合肥一中云上農舍有三處苗圃，分別位于圖中△ABC的三個頂點，已知

  AB

  =

  AC

  =

  20

  2

  m

  ，BC=40m.為了解決三個苗圃的灌溉問題，現要在△ABC區域內（不包括邊界）且與B，C等距的一點O處建立一個蓄水池，并鋪設管道OA、OB、OC．
  （1）設∠OBC=θ，記鋪設的管道總長度為ym,請將y表示為θ的函數；
  （2）當管道總長取最小值時，求θ的值．
  組卷：27引用：3難度：0.5

  解析

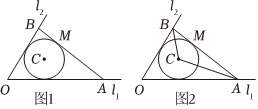• 22．如圖1，某景區是一個以C為圓心，半徑為

  3

  km

  的圓形區域，道路l₁，l₂成60°角，且均和景區邊界相切，現要修一條與景區相切的觀光木棧道AB，點A，B分別在l₁和l₂上，修建的木棧道AB與道路l₁，l₂圍成三角地塊OAB．（注：圓的切線長性質：圓外一點引圓的兩條切線長相等）．
  （1）若△OAB的面積

  S

  =

  10

  3

  k

  m

  2

  ，求木棧道AB長；
  （2）如圖2，若景區中心C與木棧道A段連線的∠CAB=α，求木棧道AB的最小值．
  組卷：61引用：2難度：0.5

  解析