2009-2010學年數學暑假作業04（必修2）

一、填空題（共14小題，每小題4分，滿分56分）

• 1．a,b,c分別表示三條直線，M表示平面，給出下列四個命題：
  ①若a∥M，b∥M，則a∥b；
  ②若b?M，a∥b,則a∥M；
  ③若a⊥c,b⊥c,則a∥b；
  ④若a⊥M，b⊥M，則a∥b.其中正確命題的個數有

  個．
  組卷：66引用：8難度：0.7

  解析

• 2．已知二面角α-l-β為60°，若平面α內有一點A到平面β的距離為

  3

  ，那么A在平面β內的射影B到平面α的距離為

  ．
  組卷：97引用：3難度：0.7

  解析

• 3．邊長為2的正方形ABCD在平面α內的射影是EFCD，如果AB與平面α的距離為

  2

  ，則AC與平面α所成角的大小是

  ．
  組卷：49引用：5難度：0.7

  解析

• 4．已知a、b是直線，α、β、γ是平面，給出下列命題：
  ①若α∥β，a?α，則a∥β；
  ②若a、b與α所成角相等，則a∥b；
  ③若α⊥β、β⊥γ，則α∥γ；
  ④若a⊥α，a⊥β，則α∥β．
  其中正確的命題的序號是

  ．
  組卷：1019引用：12難度：0.7

  解析

• 5．等體積的球和正方體，它們的表面積的大小關系是S_球

  S_正方體（填“大于、小于或等于”）．
  組卷：69引用：19難度：0.7

  解析

• 6．正三棱錐的兩個側面所成二面角α大小的取值范圍是

  ．
  組卷：45引用：2難度：0.7

  解析

二、解答題（共6小題，滿分0分）

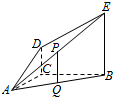• 19．如圖，DC⊥平面ABC，EB∥DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分別為AE、AB的中點．
  （Ⅰ）證明：PQ∥平面ACD；
  （Ⅱ）求異面直線AE與BC所成角的余弦值；
  （Ⅲ）求AD與平面ABE所成角的正弦值．
  組卷：967引用：8難度：0.1

  解析

• 20．如圖，四棱錐P-ABCD的底面是正方形，PD⊥底面ABCD，點E在棱PB上．
  （1）求證：平面AEC⊥平面PDB；
  （2）當PD=

  2

  AB，且E為PB的中點時，求AE與平面PDB所成的角的大小．
  組卷：1557引用：63難度：0.7

  解析