2020-2021學(xué)年上海市徐匯區(qū)位育中學(xué)高三（下）開學(xué)數(shù)學(xué)試卷

一、填空題

• 1．行列式

  1	2	3
  4	5	6
  7	8	9

  中，6的代數(shù)余子式的值是

  ．
  組卷：92引用：6難度：0.9

  解析

• 2．若拋物線

  y

  =

  1

  4

  x

  2

  上一點(diǎn)M到焦點(diǎn)F的距離為4，則點(diǎn)M的縱坐標(biāo)的值為

  ．
  組卷：93引用：4難度：0.8

  解析

• 3．設(shè)A={x|x=

  5

  k

  +

  1

  ，k∈N}，B={x|x≤5，x∈Q}，則A∩B=

  ．
  組卷：69引用：3難度：0.8

  解析

• 4．若復(fù)數(shù)z滿足（3-4i）z=|（2+i）（1-2i）|（其中i為虛數(shù)單位），則z的虛部是

  ．
  組卷：57引用：2難度：0.9

  解析

• 5．函數(shù)y=

  3

  x

  2

  x

  -

  3

  -

  4

  x

  的定義域?yàn)?!--BA-->

  ．
  組卷：118引用：2難度：0.8

  解析

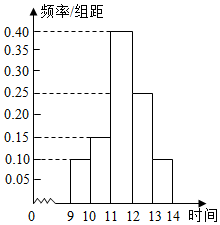• 6．某商場在國慶黃金周的促銷活動中，對10月2日9時至14時的銷售額進(jìn)行統(tǒng)計(jì)，其頻率分布直方圖如圖所示．已知9時至10時的銷售額為2.5萬元，則11時至12時的銷售額為

  萬元．
  組卷：49引用：20難度：0.7

  解析

• 7．關(guān)于x的方程lgx=

  2

  a

  +

  3

  4

  -

  a

  有大于1的實(shí)數(shù)根，則實(shí)數(shù)a的取值范圍是

  ．
  組卷：59引用：3難度：0.7

  解析

三、解答題

• 20．設(shè)復(fù)平面上點(diǎn)對應(yīng)的復(fù)數(shù)z=x+yi（x∈R，y∈R）（i為虛數(shù)單位）滿足|z+2|+|z-2|=6，點(diǎn)Z的軌跡方程為曲線C₁．雙曲線C₂：x²

  -

  y

  2

  n

  =

  1

  與曲線C₁有共同焦點(diǎn)，傾斜角為

  π

  4

  的直線l與雙曲線C₂的兩條漸近線的交點(diǎn)是A、B，

  OA

  ?

  OB

  =2，O為坐標(biāo)原點(diǎn)．
  （1）求點(diǎn)Z的軌跡方程C₁；
  （2）求直線l的方程；
  （3）設(shè)△PQR三個頂點(diǎn)在曲線C₁上，求證：當(dāng)O是△PQR重心時，△PQR的面積是定值．
  組卷：219引用：2難度：0.3

  解析

• 21．對于任意n∈N*，若數(shù)列{a_n}滿足x_n+1-x_n＞1，則稱這個數(shù)列為“K數(shù)列”．
  （1）已知數(shù)列：1，|m+1|，m²是“K數(shù)列”，求實(shí)數(shù)m的取值范圍；
  （2）設(shè)等差數(shù)列{a_n}的前n項(xiàng)和為S_n，當(dāng)首項(xiàng)a₁與公差d滿足什么條件時，數(shù)列S_n是“K數(shù)列”？
  （3）設(shè)數(shù)列{a_n}的前n項(xiàng)和為S_n，a₁=1，且2S_n+1-3S_n=2a₁，n∈N*．設(shè)c_n=λa_n+（-1）ⁿa_n+1，是否存在實(shí)數(shù)λ，使得數(shù)列{c_n}為“K數(shù)列”．若存在，求實(shí)數(shù)λ的取值范圍；若不存在，請說明理由．
  組卷：289引用：2難度：0.1

  解析