2023-2024學(xué)年廣東省東莞市石碣袁崇煥中學(xué)九年級(jí)（上）期中數(shù)學(xué)試卷

一、選擇題（每小題3分，共30分）

• 1．下列方程中，是一元二次方程的是（　　）

  A．2x+1=5	B． 1 x 2 + x - 1 = 0
  C．x2-2x=3	D．3x2+x=3x2-1
  組卷：45引用：2難度：0.9

  解析

• 2．拋物線y=x²向上平移2個(gè)單位，所得拋物線的解析式是（　　）

  A．y=x2+2

  B．y=x2-2

  C．y=（x+2）2

  D．y=（x-2）2
  組卷：329引用：5難度：0.8

  解析

• 3．一元二次方程x²+4x-4=0的根的情況是（　　）

  A．有兩個(gè)相等的實(shí)數(shù)根	B．有兩個(gè)不相等的實(shí)數(shù)根
  C．沒(méi)有實(shí)數(shù)根	D．無(wú)法確定
  組卷：55引用：3難度：0.7

  解析

• 4．已知方程x²+6x-3=0的兩根分別為x₁和x₂，則x₁+x₂等于（　　）

  A．-3

  B．3

  C．-6

  D．6
  組卷：53引用：2難度：0.7

  解析

• 5．拋物線y=-2（x-1）²+3的頂點(diǎn)坐標(biāo)是（　　）

  A．（-1，3）

  B．（1，3）

  C．（1，-3）

  D．（-1，-3）
  組卷：370引用：15難度：0.7

  解析

• 6．等腰三角形的兩邊長(zhǎng)分別是一元二次方程x²-6x+8=0的兩個(gè)根，則這個(gè)等腰三角形的周長(zhǎng)為（　　）

  A．8

  B．10

  C．8或10

  D．不能確定
  組卷：120引用：5難度：0.7

  解析

• 7．有一人患了流感，經(jīng)過(guò)兩輪傳染后共有81人患了流感．設(shè)每輪傳染中平均一人傳染了x個(gè)人，依題意所列方程正確的是（　　）

  A．x（x-1）=81	B． 1 2 x （ x - 1 ） = 81
  C．1+x+x2=81	D．1+x+（1+x）x=81
  組卷：83引用：2難度：0.5

  解析

• 8．二次函數(shù)

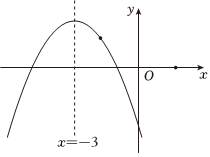  y

  =

  -

  1

  2

  x

  2

  -

  3

  x

  +

  c

  的圖象如圖所示?，若點(diǎn)A（-2，y₁），B（2，y₂）是圖象上的兩點(diǎn)，則y₁與y₂的大小關(guān)系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．不能確定
  組卷：38引用：1難度：0.7

  解析

五、解答題（三）（每小題10分，共30分）

• 24．某商場(chǎng)經(jīng)營(yíng)某種品牌的童裝，進(jìn)價(jià)為每件70元，根據(jù)市場(chǎng)調(diào)研，在一段時(shí)間內(nèi)，當(dāng)童裝的銷售定價(jià)為每件110元時(shí)，可售出20件，而每件定價(jià)每降低1元，銷售量就增加2件．
  （1）當(dāng)童裝銷售定價(jià)為每件100元時(shí)，銷售量為

  件；
  （2）直接寫出銷售量y（件）與售價(jià)x（元/件）的函數(shù)關(guān)系式為

  ；
  （3）該童裝的銷售定價(jià)為每件多少元時(shí)，商場(chǎng)銷售該品牌童裝可盈利1200元？
  組卷：204引用：4難度：0.5

  解析

• 25．如圖，一次函數(shù)

  y

  =

  -

  1

  2

  x

  +

  2

  分別交y軸、x軸于A、B兩點(diǎn)，拋物線y=-x²+bx+c過(guò)A、B兩點(diǎn)．
  （1）求這個(gè)拋物線的解析式；
  （2）作垂直x軸的直線x=t,在第一象限交直線AB于M，交這個(gè)拋物線于N．求當(dāng)t取何值時(shí)，MN有最大值？最大值是多少？
  （3）在（2）的情況下，以A、M、N、D為頂點(diǎn)作平行四邊形，求第四個(gè)頂點(diǎn)D的坐標(biāo)．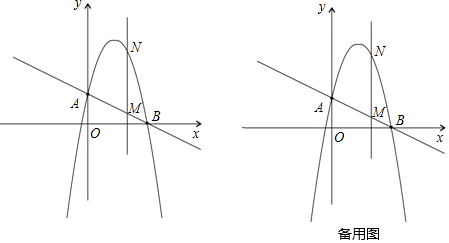
  
  組卷：2590引用：62難度：0.5

  解析