2022-2023學年廣東省深圳市南山區桃源中學九年級（上）第一次月考數學試卷

一、選擇題（每題3分，共36分）

• 1．下列四個銀行標志中，既是中心對稱圖形，又是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：1246引用：34難度：0.9

  解析

• 2．如圖，在Rt△ABC中，∠ACB=90°，∠ABC=30°，將△ABC繞點C順時針旋轉至△AB'C使得點A恰好落在AB上，則旋轉角度為（　　）

  A．30°

  B．60°

  C．90°

  D．150°
  組卷：568引用：10難度：0.6

  解析

• 3．對于二次函數y=x²-2mx-3，下列結論錯誤的是（　　）

  A．它的圖象與x軸有兩個交點

  B．方程x2-2mx=3的兩根之積為-3

  C．它的圖象的對稱軸在y軸的右側

  D．x＜m時，y隨x的增大而減小
  組卷：2133引用：12難度：0.7

  解析

• 4．已知m、n、4分別是等腰三角形（非等邊三角形）三邊的長，且m、n是關于x的一元二次方程x²-6x+k+2=0的兩個根，則k的值等于（　　）

  A．7

  B．7或6

  C．6或-7

  D．6
  組卷：2696引用：19難度：0.6

  解析

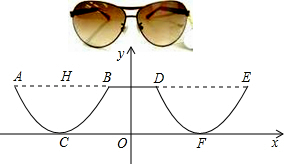• 5．為了美觀，在加工太陽鏡時將下半部分輪廓制作成拋物線的形狀（如圖所示），對應的兩條拋物線關于y軸對稱，AE∥x軸，AB=4cm,最低點C在x軸上，高CH=1cm,BD=2cm,則右輪廓DFE所在拋物線的解析式為（　　）

  A．y= 1 4 （x+3）2	B．y= 1 4 （x-3）2
  C．y=- 1 4 （x+3）2	D．y=- 1 4 （x-3）2
  組卷：1353引用：14難度：0.9

  解析

• 6．若（m²+n²）（1-m²-n²）+6=0，則m²+n²的值為（　　）

  A．3

  B．-2

  C．3或-2

  D．-3或2
  組卷：76引用：4難度：0.7

  解析

• 7．已知a,b是關于x的一元二次方程x²+（2m+3）x+m²=0的兩個不相等的實數根，且滿足

  1

  a

  +

  1

  b

  =

  -

  1

  ，則m的值是（　　）

  A．-3或1

  B．3或-1

  C．3

  D．1
  組卷：1005引用：6難度：0.6

  解析

三、解答題

• 22．如圖，一次函數

  y

  =

  -

  1

  2

  x

  +

  2

  分別交y軸、x軸于A、B兩點，拋物線y=-x²+bx+c過A、B兩點．
  （1）求這個拋物線的解析式；
  （2）作垂直x軸的直線x=t,在第一象限交直線AB于M，交這個拋物線于N．求當t取何值時，MN有最大值？最大值是多少？
  （3）在（2）的情況下，以A、M、N、D為頂點作平行四邊形，求第四個頂點D的坐標．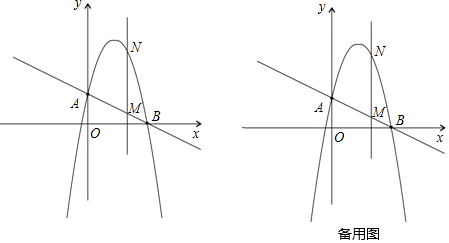
  
  組卷：2587引用：62難度：0.5

  解析

• 23．已知拋物線y=ax²+bx-4經過點A（2，0）、B（-4，0），與y軸交于點C．
  （1）求這條拋物線的解析式；
  （2）如圖1，點P是第三象限內拋物線上的一個動點，當四邊形ABPC的面積最大時，求點P的坐標；
  （3）如圖2，線段AC的垂直平分線交x軸于點E，垂足為D，M為拋物線的頂點，在直線DE上是否存在一點G，使△CMG的周長最小？若存在，求出點G的坐標；若不存在，請說明理由．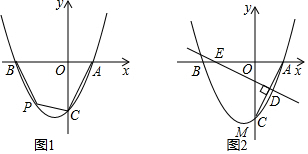
  
  組卷：3632引用：10難度：0.3

  解析