2013-2014學年浙江省金華中學九年級（上）入學數學試卷

一、選擇題（每小題4分，共40分）

• 1．添加下列條件，不能使?ABCD是矩形的是（　　）

  A．OA=OC，OB=OD	B．AC=BD
  C．OA=OB	D．∠ABC=90°
  組卷：72引用：1難度：0.9

  解析

• 2．順次連接等腰梯形各邊中點所圍成的四邊形是（　　）

  A．平行四邊形

  B．矩形

  C．菱形

  D．正方形
  組卷：541引用：53難度：0.9

  解析

• 3．如果ab＞0  bc＜0 那么y=-

  a

  b

  x-

  c

  b

  不經過（　　）象限．

  A．一

  B．二

  C．三

  D．四
  組卷：114引用：1難度：0.9

  解析

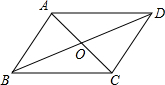• 4．如圖，在平行四邊形ABCD中，AB=3cm,BC=5cm,對角線AC，BD相交于點O，則OA的取值范圍是（　　）

  A．2cm＜OA＜5cm

  B．2cm＜OA＜8cm

  C．1cm＜OA＜4cm

  D．3cm＜OA＜8cm
  組卷：1322引用：36難度：0.9

  解析

• 5．方程

  1

  x

  +

  4

  -

  2

  x

  +

  3

  =

  3

  x

  +

  2

  -

  4

  x

  +

  1

  的解為（　　）

  A．x=-5	B．x=- 5 2
  C．x1=-5，x2=- 5 2	D．無解
  組卷：45引用：1難度：0.9

  解析

• 6．已知

  1

  a

  +

  1

  b

  =

  5

  a

  +

  b

  ，則

  b

  a

  +

  a

  b

  的值是（　　）

  A．5

  B．7

  C．3

  D． 1 3
  組卷：187引用：3難度：0.9

  解析

• 7．已知

  2

  x

  -

  3

  x

  2

  -

  x

  =

  A

  x

  -

  1

  +

  B

  x

  ，其中A，B為常數，那么A+B的值為（　　）

  A．-2

  B．2

  C．-4

  D．4
  組卷：218引用：4難度：0.7

  解析

• 8．已知a=3⁵⁵，b=4⁴⁴，c=5³³，則有（　　）

  A．a＜b＜c

  B．c＜b＜a

  C．c＜a＜b

  D．a＜c＜b
  組卷：1023引用：16難度：0.9

  解析

三、解答題（每題12分．共60分）

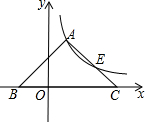• 24．如圖，動點A（a,b）在雙曲線y=

  6

  x

  （x＞0）圖象上，以A為直角頂點作等腰Rt△ABC（點B在C的左側，且均在x軸上）．
  （1）請直接寫出a?b的值；
  （2）若B（-1，0），且a、b都為整數時，試求線段BC的長．
  （3）直線AC與雙曲線y=

  6

  x

  （x＞0）圖象交于另一點E．問：在點A整個運動過程中，AC?EC的值是否會發生變化？若不會，請求出它的值；若會，請說明理由．
  組卷：86引用：3難度：0.5

  解析

• 25．如圖所示，在矩形ABCD中，AB=12cm,BC=5cm,點P沿AB邊從點A開始向點B以2cm/s的速度移動；點Q沿DA邊從點D開始向點A以1cm/s的速度移動．如果P、Q同時出發，當Q到達終點時，P也隨之停止運動．用t表示移動時間，設四邊形QAPC的面積為S．
  （1）試用t表示AQ、BP的長；
  （2）試求出S與t的函數關系式；
  （3）當t為何值時，△QAP為等腰直角三角形？并求出此時S的值．
  組卷：370引用：7難度：0.3

  解析