2022-2023學年山東省濱州市高新高級中學高二（下）期中數學試卷

一、單選題（本大題共8小題，共40分．在每小題列出的選項中，選出符合題目的一項）

• 1．已知集合A={-1，1，2，4}，B={x||x-1|≤1}，則A∩B=（　　）

  A．{-1，2}

  B．{1，2}

  C．{1，4}

  D．{-1，4}
  組卷：4248引用：36難度：0.9

  解析

• 2．命題“?x∈R，x＞sinx”的否定是（　　）

  A．?x∈R，x≤sinx	B．?x∈R，x≥sinx
  C．?x∈R，x＞sinx	D．?x∈R，x≤sinx
  組卷：128引用：2難度：0.8

  解析

• 3．已知a,b,c,d∈R，則下列命題中一定成立的是（　　）

  A．若a＞b,c＞d,則a+b＞c+d	B．若a2＞b2，則-a＜-b
  C．若a＞b,c＜d,則 a c ＞ b d	D．若a＞-b,則c-a＜c+b
  組卷：318引用：3難度：0.8

  解析

• 4．設x∈R，則“x²-5x＜0”是“|x-1|＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：817引用：26難度：0.8

  解析

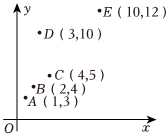• 5．有一散點圖如圖所示，在5個數據（x,y）中去掉D（3，10）后，下列說法正確的是（　　）

  A．相關系數r變小

  B．殘差平方和變小

  C．變量x,y負相關

  D．解釋變量x與預報變量y的相關性變弱
  組卷：36引用：7難度：0.7

  解析

• 6．若函數f（x）滿足f（x）+2f（

  1

  x

  ）=2x+1，則f（2）=（　　）

  A．- 1 3

  B． 2 3

  C． 8 3

  D． 1 2
  組卷：65引用：2難度：0.9

  解析

• 7．已知離散型隨機變量X服從二項分布X～B（n,p），且E（X）=4，D（X）=q,則

  1

  p

  +

  1

  q

  的最小值為（　　）

  A．2

  B． 5 2

  C． 9 4

  D．4
  組卷：1807引用：9難度：0.4

  解析

四、解答題（本大題共6小題，共70分．其中，第17題10分，其余各題12分；解答應寫出文字說明，證明過程或演算步驟）

• 21．為迎接建黨一百周年，在全縣中小學校開展“恰是百年風華，愛我山河美景”競賽考試活動，進一步激發學生的愛國熱情．某中學于2021年3月份對全校學生進行了“建黨一百周年”國防教育知識競賽考試，并隨機抽取了100名學生的成績進行了統計，其中男女生各占一半，繪制了頻率分布直方圖（如圖所示），規定80分（滿分100分）及以上者為成績優秀，否則為成績不優秀．
  （1）求圖中a的值；
  （2）根據已知條件完成下面2×2列聯表，并判斷能否有95%的把握認為“成績優秀”與性別有關？
  

  	成績優秀	成績不優秀	合計
  男	17
  女			50
  合計

  （3）將頻率視為概率，從本次考試的全縣所有學生中，隨機抽取4人去其他學校進行愛國勵志演講宣傳，記抽取的4人中成績優秀的人數為X，求X的分布列和數學期望．
  附：
  

  P（K2≥k）	…	0.10	0.05	0.025	0.010	0.001
  k	…	2.706	3.841	5.024	6.635	10.828

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ．
  組卷：60引用：4難度：0.5

  解析

• 22．近年來，我國大學生畢業人數呈逐年上升趨勢，各省市出臺優惠政策鼓勵高校畢業生自主創業，以創業帶動就業．某市統計了該市其中四所大學2021年的畢業生人數及自主創業人數（單位：千人），得到如下表格：
  

  	A大學	B大學	C大學	D大學
  當年畢業人數x（千人）	3	4	5	6
  自主創業人數y（千人）	0.1	0.2	0.4	0.5

  （1）已知y與x具有較強的線性相關關系，求y關于x的線性回歸方程

  ?

  y

  =

  ?

  a

  +

  ?

  b

  x

  ；
  （2）假設該市政府對選擇自主創業的大學生每人發放1萬元的創業補貼．
  （ⅰ）若該市E大學2021年畢業生人數為7千人，根據（1）的結論估計該市政府要給E大學選擇自主創業的畢業生創業補貼的總金額；
  （ⅱ）若A大學的畢業生中小明、小紅選擇自主創業的概率分別為p,

  2

  p

  -

  1

  （

  1

  2

  ＜

  p

  ＜

  1

  ）

  ，該市政府對小明、小紅兩人的自主創業的補貼總金額的期望不超過1.4萬元，求p的取值范圍．
  參考公式：回歸方程

  ?

  y

  =

  ?

  a

  +

  ?

  b

  x

  中斜率和截距的最小二乘法估計公式分別為

  ?

  b

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  xy

  n

  ∑

  i

  =

  1

  x

  2

  i

  -

  n

  x

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ．
  組卷：85引用：3難度：0.5

  解析