2023-2024學年山東省濟南一中高二（上）月考數學試卷（10月份）

一、單選題

• 1．已知直線過點（1，2），且縱截距為橫截距的兩倍，則直線l的方程為（　　）

  A．2x-y=0	B．2x+y-4=0
  C．2x-y=0或x+2y-2=0	D．2x-y=0或2x+y-4=0
  組卷：971引用：28難度：0.8

  解析

• 2．過點（-2，0）與圓x²+y²-4x-m=0相切的兩條直線垂直，則m=（　　）

  A．-4

  B． - 2 2

  C． 2 2

  D．4
  組卷：489引用：7難度：0.7

  解析

• 3．如果方程x²+ky²=2表示焦點在y軸上的橢圓，那么實數k的取值范圍是（　　）

  A．（1，+∞）

  B．（1，2）

  C．（ 1 2 ，1）

  D．（0，1）
  組卷：317引用：12難度：0.7

  解析

• 4．阿波羅尼斯是古希臘著名數學家，與阿基米德、歐幾里得并稱為亞歷山大時期數學三巨匠，他研究發現：如果一個動點P到兩個定點的距離之比為常數λ（λ＞0，且λ≠1），那么點P的軌跡為圓，這就是著名的阿波羅尼斯圓．若點C到A（-1，0），B（1，0）的距離之比為

  3

  ，則點C到直線x-2y+8=0的距離的最小值為（　　）

  A． 2 5 - 3

  B． 5 - 3

  C． 2 5

  D． 3
  組卷：214引用：10難度：0.5

  解析

• 5．設x,y∈R，向量

  a

  =（x,1，1），

  b

  =（1，y,1），

  c

  =（2，-4，2），且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，則|

  a

  +

  b

  |=（　　）

  A． 2 2

  B． 10

  C．3

  D．4
  組卷：2726引用：77難度：0.8

  解析

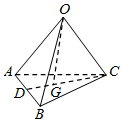• 6．如圖，G是△ABC的重心，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，則

  OG

  =（　　）

  A． 1 3 a + 2 3 b + 2 3 c	B． 2 3 a + 2 3 b + 1 3 c
  C． 2 3 a + 2 3 b + 2 3 c	D． 1 3 a + 1 3 b + 1 3 c
  組卷：54引用：14難度：0.9

  解析

• 7．已知兩定點A（-3，5），B（2，8），動點P在直線x-y+1=0上，則|PA|+|PB|的最小值為（　　）

  A．5 13

  B． 34

  C．5 5

  D． 2 26
  組卷：1747引用：12難度：0.7

  解析

• 8．在下列四個命題中：
  ①若向量

  a

  ，

  b

  所在的直線為異面直線，則向量

  a

  ，

  b

  一定不共面；
  ②向量

  a

  =

  （

  2

  ，-

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  4

  ，

  2

  ，

  m

  ）

  ，若

  a

  與

  b

  的夾角為鈍角，則實數m的取值范圍為m＜5；
  ③直線

  x

  a

  +

  y

  b

  =

  1

  的一個方向向量為

  （

  1

  ，-

  b

  a

  ）

  ；
  ④若存在不全為0的實數x,y,z使得

  x

  a

  +

  y

  b

  +

  z

  c

  =

  0

  ，則

  a

  ，

  b

  ，

  c

  共面．
  其中正確命題的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：205引用：5難度：0.6

  解析

四、解答題

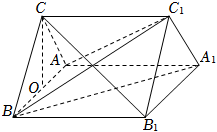• 23．如圖，直三棱柱ABC-A₁B₁C₁中，ABC是邊長為2的正三角形，O為AB的中點．
  （1）證明：CO⊥平面ABB₁A₁；
  （2）若直線B₁C與平面ABB₁A₁所成的角的正切值為

  15

  5

  ，求平面A₁BC₁與平面ABC₁夾角的余弦值．
  組卷：132引用：8難度：0.4

  解析

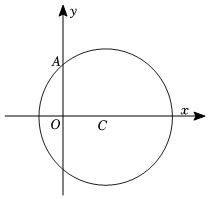• 24．已知圓C的圓心坐標為C（3，0），且該圓經過點A（0，4）．
  （1）求圓C的標準方程；
  （2）若點B也在圓C上，且弦AB長為8，求直線AB的方程；
  （3）直線l交圓C于M，N兩點，若直線AM，AN的斜率之積為2，求證：直線l過一個定點，并求出該定點坐標．
  組卷：246引用：8難度：0.4

  解析