2023-2024學(xué)年河南省洛陽市洛寧第一高級中學(xué)高三（上）第二次月考數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分．

• 1．已知全集I=R，M={x|x＜1}，N={x|log₂x＜1}，則（?_IM）∩N=（　　）

  A．[1，+∞）

  B．[1，2）

  C．（1，+∞）

  D．（1，2）
  組卷：67引用：11難度：0.7

  解析

• 2．命題“?a∈[0.1]，a⁴+a²＞1”的否定是（　　）

  A．?a?[0，1]，a4+a2＞1	B．?a∈[0，1]，a4+a2≤1
  C．?a∈[0，1]，a4+a2＞1	D．?a∈[0，1]，a4+a2≤1
  組卷：472引用：22難度：0.8

  解析

• 3．已知

  x

  =

  π

  3

  ，x=π是函數(shù)

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  π

  2

  ＜

  φ

  ＜

  3

  π

  2

  ）

  圖象上兩條相鄰的對稱軸，則φ=（　　）

  A．π

  B． 3 π 4

  C． 2 π 3

  D． π 3
  組卷：178引用：5難度：0.5

  解析

• 4．已知向量

  a

  =

  （

  1

  ，

  3

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，

  c

  =

  （

  4

  ，

  5

  ）

  ．若

  a

  與

  b

  +

  λ

  c

  垂直，則實(shí)數(shù)λ的值為（　　）

  A． 2 19

  B． 4 11

  C．2

  D． - 4 7
  組卷：605引用：6難度：0.8

  解析

• 5．函數(shù)

  f

  （

  x

  ）

  =

  （

  1

  -

  e

  x

  1

  +

  e

  x

  ）

  cos

  （

  π

  2

  -

  x

  ）

  的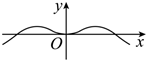部分圖象大致形狀是（　　）

  A．

  B．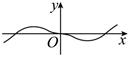

  C．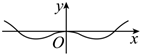

  D．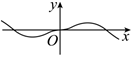
  組卷：235引用：11難度：0.6

  解析

• 6．若α，β為銳角，且

  α

  +

  β

  =

  π

  4

  ，則tanα+tanβ的最小值為（　　）

  A． 2 2 - 2

  B． 2 - 1

  C． 2 3 - 2

  D． 3 - 1
  組卷：534引用：10難度：0.5

  解析

• 7．在數(shù)列{a_n}中，如果存在非零的常數(shù)T，使得a_n+T=a_n對于任意正整數(shù)n均成立，那么就稱數(shù)列{a_n}為周期數(shù)列，其中T叫做數(shù)列{a_n}的周期．已知數(shù)列{x_n}滿足x_n+2=|x_n+1-x_n|（x∈N^*），若x₁=1，x₂=a（a≤1，a≠0），當(dāng)數(shù)列{x_n}的周期為3時(shí)，則數(shù)列{x_n}的前2024項(xiàng)的和S₂₀₂₄為（　　）

  A．676

  B．675

  C．1350

  D．1349
  組卷：46引用：5難度：0.6

  解析

三、解答題：共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

• 21．已知函數(shù)f（x）=2xcosx,g（x）=（a-1）x-

  x

  3

  2

  ，x∈[0，1]．
  （1）當(dāng)a=2時(shí)，求證：f（x）≥2g（x）；
  （2）若f（x）≤g（x）對x∈[0，1]恒成立，求實(shí)數(shù)a的取值范圍．
  組卷：50引用：3難度：0.4

  解析

• 22．已知函數(shù)f（x）=

  e

  x

  x

  -lnx+x
  （1）討論函數(shù)f（x）的單調(diào)性；
  （2）若不等式g（x）=x²?f（x）+（x²-1）lnx-x³-x≤t有解，求實(shí)數(shù)t的取值范圍；
  （3）若函數(shù)h（x）=f（x）-a（a∈R）有兩個(gè)零點(diǎn)x₁，x₂，證明：x₁?x₂＜1．
  組卷：128引用：3難度：0.5

  解析