2023年重慶市巴蜀中學(xué)高考數(shù)學(xué)適應(yīng)性試卷（五）

一、單項(xiàng)選擇題（本大題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）

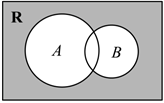• 1．已知全集是實(shí)數(shù)集R，集合A={x|x＞2}，B={x|x²-4x-12＞0}，則圖中陰影部分所表示的集合為（　　）

  A．{x|x＞2}

  B．{x|-2≤x≤2}

  C．{x|x≤2}

  D．{x|x＜-2或x＞2}
  組卷：99引用：2難度：0.7

  解析

• 2．已知復(fù)數(shù)z₁，z₂是方程z²-z+1=0的兩個(gè)虛數(shù)根，則z₁，z₂在夏平面內(nèi)對(duì)應(yīng)的點(diǎn)關(guān)于（　　）

  A．原點(diǎn)對(duì)稱	B．直線y=x對(duì)稱
  C．y軸對(duì)稱	D．x軸對(duì)稱
  組卷：96引用：2難度：0.7

  解析

• 3．已知定義在R上的函數(shù)f（x）滿足f（3）=-2，且h（x）=-x²+f（3x）為奇函數(shù)，則f（-3）=（　　）

  A．4

  B．-2

  C．0

  D．2
  組卷：190引用：2難度：0.7

  解析

• 4．圓臺(tái)上、下底面圓的圓周都在一個(gè)半徑為5的球面上，其上、下底面圓的周長(zhǎng)分別為8π和10π，則該圓臺(tái)的側(cè)面積為（　　）

  A． 8 10 π

  B． 8 11 π

  C． 9 10 π

  D． 9 11 π
  組卷：198引用：2難度：0.7

  解析

• 5．已知{a_n}為遞增等差數(shù)列，等比數(shù)列{b_n}以a₁，a₂為前兩項(xiàng)且公比為3，若b₅=a_m，則m=（　　）

  A．13

  B．41

  C．57

  D．86
  組卷：82引用：3難度：0.7

  解析

• 6．化簡(jiǎn)4sin160°+tan20°=（　　）

  A． 3

  B． 4 3

  C． 2 3

  D． 4 3 3
  組卷：386引用：2難度：0.6

  解析

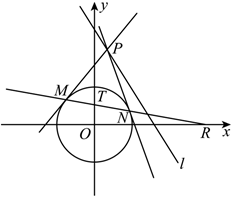• 7．如圖，已知直線l：2x+y+m=0與圓O：x²+y²=2相離，點(diǎn)P在直線l上運(yùn)動(dòng)且位于第一象限，過(guò)P作圓O的兩條切線，切點(diǎn)分別是M，N，直線MN與x軸、y軸分別交于R，T兩點(diǎn)，且△ORT面積的最小值為

  16

  25

  ，則m的值為（　　）

  A．-4

  B．-9

  C．-6

  D．-5
  組卷：170引用：3難度：0.5

  解析

四、解答題（共70分，解答應(yīng)寫(xiě)出文字說(shuō)明公眾號(hào)山城學(xué)術(shù)圈，證明過(guò)程或演算步驟）

• 21．設(shè)雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，離心率為

  5

  ，P是雙曲線C上的一點(diǎn)，且F₁P⊥F₂P，△PF₁F₂的面積為4．
  （1）求雙曲線C的方程；
  （2）A₁，A₂分別是雙曲線C的左、右頂點(diǎn)，T是雙曲線C上異于A₁，A₂的一個(gè)動(dòng)點(diǎn)，直線TA₁，TA₂分別與直線x=

  1

  2

  交于Q₁，Q₂兩點(diǎn)，問(wèn)以Q₁Q₂為直徑的圓是否過(guò)定點(diǎn)？若是，求出此定點(diǎn)；若不是，請(qǐng)說(shuō)明理由．
  組卷：190引用：3難度：0.5

  解析

• 22．若函數(shù)f（x）=（1-x）lnx-ax,a∈R有兩個(gè)零點(diǎn)．
  （1）求證：a＜0；
  （2）設(shè)x₀為函數(shù)f（x）的極大值點(diǎn)，x₁為函數(shù)f（x）的零點(diǎn)，且x₁＜x₀，求證：

  2

  x

  0

  +

  x

  1

  ＞

  2

  2

  ．
  組卷：83引用：2難度：0.4

  解析