2022-2023學年黑龍江省雙鴨山市八年級（下）期末數學試卷

一、選擇題（每題3分，滿分30分）

• 1．下列各式計算正確的是（　　）

  A． 24 ÷ 6 = 4

  B． 54 ÷ 9 = 6

  C． 30 ÷ 6 = 5

  D． 4 7 ÷ 1 49 = 7 2
  組卷：179引用：4難度：0.7

  解析

• 2．滿足下列條件的△ABC，其中不是直角三角形的是（　　）

  A．b2=（a+c）（a-c）	B．a：b：c=1： 3 ：2
  C．∠C=∠A-∠B	D．∠A：∠B：∠C=3：4：5
  組卷：101引用：5難度：0.5

  解析

• 3．某校男子足球隊的年齡分布如下表：
  

  年齡/歲	13	14	15	16	17	18
  人數	2	6	8	3	2	1

  則這些隊員年齡的平均數是（　　）

  A．13

  B．14

  C．14.5

  D．15
  組卷：107引用：6難度：0.5

  解析

• 4．在同一平面直角坐標系中，一次函數的y₁=ax+b與y₂=bx+a圖象可能是（　　）

  A．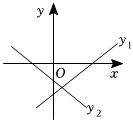

  B．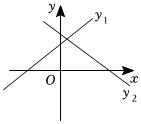

  C．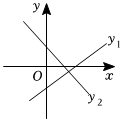

  D．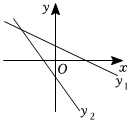
  組卷：377引用：5難度：0.5

  解析

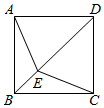• 5．如圖，在正方形ABCD中，點E是對角線上一點，連接AE，CE，若DE=AB，則∠AEC的度數為（　　）

  A．105°

  B．120°

  C．135°

  D．150°
  組卷：395引用：5難度：0.5

  解析

• 6．我們規定：對于任意的正數m,n的運算“Φ”為當m＜n時，mΦn=2

  m

  +

  n

  ；當m≥n時，mΦn=2

  m

  -

  n

  ，其他運算符號意義不變，按上述規定，計算（3Φ2）-（8Φ12）的結果為（　　）

  A． 5 2

  B． - 5 2

  C． 4 2

  D． - 4 2
  組卷：327引用：8難度：0.5

  解析

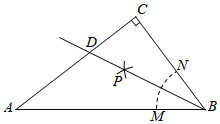• 7．如圖，在Rt△ABC中，∠ACB=90°，按以下步驟作圖：①以B為圓心，任意長為半徑作弧，分別交BA、BC于M、N兩點；②分別以M、N為圓心，以大于

  1

  2

  MN的長為半徑作弧，兩弧相交于點P；③作射線BP，交邊AC于D點．若AB=10，BC=6，則線段CD的長為（　　）

  A．3

  B． 10 3

  C． 8 3

  D． 16 5
  組卷：1808引用：32難度：0.7

  解析

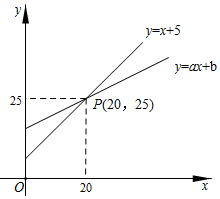• 8．數形結合是解決數學問題常用的思想方法．如圖，直線y=x+5和直線y=ax+b相交于點P，根據圖象可知，方程x+5=ax+b的解是（　　）

  A．x=20

  B．x=5

  C．x=25

  D．x=15
  組卷：4305引用：51難度：0.6

  解析

三、解答題（滿分66分）

• 25．（1）【感知】如圖①，四邊形ABCD、CEFG均為正方形．BE與DG的數量關系為

  ．
  （2）【拓展】如圖②，四邊形ABCD、CEFG均為菱形，且∠A=∠F．請判斷BE與DG的數量關系，并說明理由
  （3）【應用】如圖③，四邊形ABCD、CEFG均為菱形，點E在邊AD上，點G在AD延長線上．若AE=2ED，∠A=∠F，△EBC的面積為9，則菱形CEFG的面積為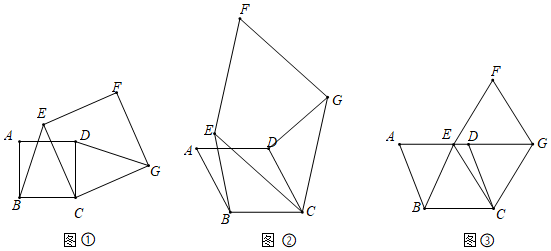

  ．
  
  組卷：453引用：8難度：0.3

  解析

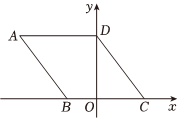• 26．如圖所示，在平面直角坐標系中，四邊形ABCD是菱形，點A的坐標為（-5，4），點B，C在x軸上，點D在y軸上．
  （1）求點B的坐標；
  （2）動點P以每秒1個單位長度的速度從點O出發，沿射線OB方向運動，設點P運動的時間為t秒，連接PD，BD，設△PBD的面積為S（S≠0），求S與t的函數關系式（請直接寫出自變量t的取值范圍）；
  （3）在（2）的條件下，平面內是否存在點Q，使以A，C，P，Q為頂點的四邊形為矩形？若存在，請直接寫出點Q的坐標；若不存在，請說明理由．
  組卷：100引用：5難度：0.5

  解析