2013-2014學年四川省成都七中高三（下）第二次周練數學試卷（文科）（5月份）

一、選擇題（共50分，每題5分）

• 1．設A={x|x²-1＞0}，B={x|log₂x＜0}，則A∩B=（　　）

  A．{x|x＞1}

  B．{x|x＞0}

  C．{x|x＜-1}

  D．?
  組卷：10引用：5難度：0.9

  解析

• 2．設i是虛數單位，若（a+bi）（1+i）=2（1-i），其中a,b∈R，則a+b的值是（　　）

  A． - 1 2

  B．-2

  C．2

  D． 3 2
  組卷：15引用：3難度：0.9

  解析

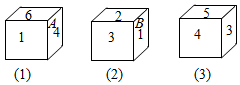• 3．有一正方體，六個面上分別寫有數字1、2、3、4、5、6，有三個人從不同的角度觀察的結果如圖所示．如果記3的對面的數字為m,4的對面的數字為n,那么m+n的值為（　　）

  A．8

  B．7

  C．6

  D．5
  組卷：104引用：14難度：0.7

  解析

• 4．設a=|log₅4|，b=|log₅（2-

  3

  ）|，c=|log₄

  17

  |，則（　　）

  A．a＜c＜b

  B．b＜c＜a

  C．a＜b＜c

  D．b＜a＜c
  組卷：308引用：3難度：0.9

  解析

• 5．已知A，B，C是銳角△ABC的三個內角，向量

  p

  =（sinA，1），

  q

  =（1，-cosB），則

  p

  與

  q

  的夾角是（　　）

  A．銳角

  B．鈍角

  C．直角

  D．不確定
  組卷：68引用：10難度：0.9

  解析

• 6．下列判斷錯誤的是（　　）

  A．“am2＜bm2”是“a＜b”的充分不必要條件

  B．“x3-x2-1≤0對x∈R恒成立”的否定是“存在x0∈R使得x03-x02-1＞0”

  C．若“p∧q”為假命題，則p,q均為假命題

  D．若隨機變量ξ服從二項分布：ξ～B（4， 1 4 ），則Eξ=1
  組卷：12引用：3難度：0.9

  解析

• 7．設ω＞0，函數y=sin（ωx+

  π

  3

  ）+2的圖象向右平移

  4

  π

  3

  個單位后與原圖象重合，則ω的最小值是（　　）

  A． 2 3

  B． 4 3

  C． 3 2

  D．3
  組卷：1526引用：80難度：0.9

  解析

三、解答題（共75分）

• 20．橢圓Γ：

  x

  2

  25

  +

  y

  2

  r

  2

  =1（r＞0）的左頂點為A，直線x=4交橢圓Γ于B，C兩點（C上B下），動點P和定點D（-4，6）都在橢圓Γ上．
  （1）求橢圓方程及四邊形ABCD的面積；
  （2）若四邊形ABCP為梯形，求點P的坐標；
  （3）若m,n為實數，

  BP

  =m

  BA

  +n

  BC

  ，求m+n的取值范圍．
  組卷：44引用：3難度：0.1

  解析

• 21．已知函數f（x）=2sinx-x,g（x）=f（x）-（2-

  π

  2

  ）．
  （1）討論g（x）在（0，

  π

  6

  ）內和在（

  π

  6

  ，

  π

  2

  ）內的零點情況．
  （2）設x₀是g（x）在（0，

  π

  6

  ）內的一個零點，求f（x）在[x₀，

  π

  2

  ]上的最值．
  （3）證明對n∈N^*恒有n-

  n

  +

  1

  2

  ＜

  n

  ∑

  k

  =

  1

  cos

  1

  k

  ＜（

  3

  2

  +

  π

  12

  ）n-

  n

  +

  1

  +1．
  組卷：48引用：2難度：0.1

  解析