當前位置：試卷中心 > 試卷詳情

2022-2023學年吉林省長春十一中高一（上）月考數學試卷

發布：2024/8/10 12:0:4

一、選擇題：本題共8小題，每小題5分．在每小題給出的四個選項中，只有一個選項是符合題目要求的．

1．已知集合
P
=
{
x
|
y
=
x
-
1
}
，集合
Q
=
{
y
|
y
=
x
2
+
1
}
，則P與Q的關系是（　　）
A．P?Q B．P=Q
C．Q?P D．以上都不正確
組卷：10引用：1難度：0.7
解析
2．下列不等式恒成立的是（　　）
A．a²+b²≤2ab B．a²+b²≥-2ab C．a+b≥-2
|
ab
|
D．a+b≤2
|
ab
|
組卷：762引用：22難度：0.8
解析
3．已知函數f（x）=2^x+x,g（x）=x+log₂x,h（x）=x³+x的零點分別為x₁，x₂，x₃，則（　　）
A．x₁＜x₃＜x₂ B．x₂＜x₁＜x₃ C．x₁＜x₂＜x₃ D．x₃＜x₁＜x₂
組卷：84引用：3難度：0.6
解析
4．關于函數f（x）=lg
x
2
+
1
|
x
|
（x≠0，x∈R），有下列命題：
①函數y=f（x）的圖象關于y軸對稱；
②當-1＜x＜0或x＞1時，f（x）為增函數；
③f（x）無最大值，也無最小值．
其中正確命題的個數是（　　）
A．0個 B．1個 C．2個 D．3個
組卷：171引用：4難度：0.6
解析
5．若sin（α-β）cosα-cos（α-β）sinα=m,且β為第三象限角，則cosβ的值為（　　）
A．
1
-
m
2
B．-
1
-
m
2
C．
m
2
-
1
D．-
m
2
-
1
組卷：447引用：19難度：0.9
解析
6．在△ABC中，tanA+tanB+
3
=
3
tanAtanB，則C等于（　　）
A．
π
3
B．
2
π
3
C．
π
6
D．
π
4
組卷：1252引用：25難度：0.9
解析
7．已知函數
f
（
x
）
=
2
sin
（
2
x
+
π
6
）
，對于任意的
a
∈
[
-
3
，
1
）
，方程f（x）=a（0＜x≤m）恰有一個實數根，則m的取值范圍為（　　）
A．
（
7
π
12
，
3
π
4
]
B．
[
π
2
，
5
π
6
）
C．
（
π
2
，
5
π
6
]
D．
[
7
π
12
，
3
π
4
）
組卷：261引用：8難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．

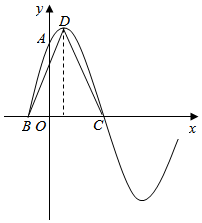21．已知函數f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的部分圖象如圖．該圖象與y軸交于點A（0，
3
），與x軸交于點B，C兩點，D為圖象的最高點，且△BCD的面積為
π
2
．
（1）求f（x）的解析式及其單調遞增區間；
（2）若將f（x）的圖象向右平移
π
12
個單位，再將所得圖象上所有點的橫坐標伸長為原來的2倍（縱坐標不變），得到函數g（x）的圖象，若g（α）=
8
5
（
π
2
＜α＜π），求sin（α+
5
π
12
）的值．
組卷：168引用：4難度：0.6
解析
22．已知函數
f
（
x
）
=
x
2
-
2
mx
+
2
，
g
（
x
）
=
2
sin
（
ωx
-
π
6
）
（
ω
＞
0
）
，且g（x）在[0，π]上單調遞增．
（1）若
g
（
x
）
≥
g
（
-
2
π
3
）
恒成立，求ω的值；
（2）在（1）的條件下，若當x₁∈[0，2]時，總有
x
2
∈
[
0
，
4
π
3
]
使得f（x₁）=g（x₂），求實數m的取值范圍．
組卷：84引用：5難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．P?Q	B．P=Q
C．Q?P	D．以上都不正確

2022-2023學年吉林省長春十一中高一（上）月考數學試卷

一、選擇題：本題共8小題，每小題5分．在每小題給出的四個選項中，只有一個選項是符合題目要求的．

1．已知集合P={x|y=x-1}，集合Q={y|y=x2+1}，則P與Q的關系是（ ）

2．下列不等式恒成立的是（ ）

3．已知函數f（x）=2x+x,g（x）=x+log2x,h（x）=x3+x的零點分別為x1，x2，x3，則（ ）

4．關于函數f（x）=lgx2+1|x|（x≠0，x∈R），有下列命題：①函數y=f（x）的圖象關于y軸對稱；②當-1＜x＜0或x＞1時，f（x）為增函數；③f（x）無最大值，也無最小值．其中正確命題的個數是（ ）

5．若sin（α-β）cosα-cos（α-β）sinα=m,且β為第三象限角，則cosβ的值為（ ）

6．在△ABC中，tanA+tanB+3=3tanAtanB，則C等于（ ）

7．已知函數f（x）=2sin（2x+π6），對于任意的a∈[-3，1），方程f（x）=a（0＜x≤m）恰有一個實數根，則m的取值范圍為（ ）

四、解答題：本題共6小題，共70分．

1．已知集合
P
=
{
x
|
y
=
x
-
1
}
，集合
Q
=
{
y
|
y
=
x
2
+
1
}
，則P與Q的關系是（　　）

2．下列不等式恒成立的是（　　）

3．已知函數f（x）=2^x+x,g（x）=x+log₂x,h（x）=x³+x的零點分別為x₁，x₂，x₃，則（　　）

4．關于函數f（x）=lg
x
2
+
1
|
x
|
（x≠0，x∈R），有下列命題：
①函數y=f（x）的圖象關于y軸對稱；
②當-1＜x＜0或x＞1時，f（x）為增函數；
③f（x）無最大值，也無最小值．
其中正確命題的個數是（　　）

5．若sin（α-β）cosα-cos（α-β）sinα=m,且β為第三象限角，則cosβ的值為（　　）

6．在△ABC中，tanA+tanB+
3
=
3
tanAtanB，則C等于（　　）

7．已知函數
f
（
x
）
=
2
sin
（
2
x
+
π
6
）
，對于任意的
a
∈
[
-
3
，
1
）
，方程f（x）=a（0＜x≤m）恰有一個實數根，則m的取值范圍為（　　）