2023-2024學年貴州省貴陽一中高三（上）適應性數學試卷（一）

一、單項選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．已知集合A={x|y=ln（1-x）}，

  B

  =

  {

  x

  |

  x

  -

  1

  x

  ≤

  0

  }

  ，則A∩B=（　　）

  A．{x|0＜x＜1}

  B．{x|0≤x＜1}

  C．{x|0≤x≤1}

  D．{x|0＜x≤1}
  組卷：22引用：3難度：0.5

  解析

• 2．“x＞0”是“x+

  1

  x

  ≥2”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：115引用：3難度：0.8

  解析

• 3．若隨機變量X～N（10，2²），則下列選項錯誤的是（　　）

  A．P（X≥10）=0.5	B．P（X≤8）+P（X≤12）=1
  C．P（8≤X≤12）=2P（8≤X≤10）	D．D（2X+1）=8
  組卷：130引用：2難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  （

  x

  2

  +

  1

  ）

  sin

  |

  x

  |

  e

  2

  的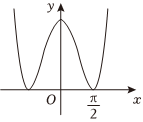圖象大致為（　　）

  A．

  B．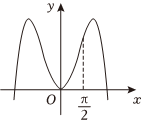

  C．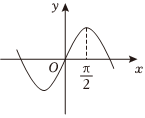

  D．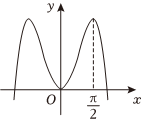
  組卷：192引用：4難度：0.7

  解析

• 5．二次函數f（x）=ax²+2（a-1）x+2在區間（-∞，4）上為減函數，則a的取值范圍為（　　）

  A． （ 1 5 ， + ∞ ）

  B． [ 0 ， 1 5 ]

  C． （ - ∞ ， 1 5 ]

  D． （ 0 ， 1 5 ]
  組卷：598引用：5難度：0.8

  解析

• 6．若過雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一個焦點作雙曲線的一條漸近線的垂線，垂線交y軸于點（0，3c）（c為雙曲線的半焦距），則此雙曲線的離心率是（　　）

  A． 3

  B． 2 2 3

  C． 10 3

  D． 10
  組卷：135引用：2難度：0.6

  解析

• 7．若

  2

  a

  +

  lo

  g

  2

  a

  ＜

  2

  2

  b

  +

  lo

  g

  2

  b

  +

  1

  ，則（　　）

  A．ln（2b-a+1）＜0	B．ln（2b-a+1）＞0
  C．ln|a-2b|＞0	D．ln|a-2b|＜0
  組卷：59引用：12難度：0.6

  解析

四、解答題（共70分.解答應寫出文字說明，證明過程或演算步驟）

• 21．馬爾科夫鏈是概率統計中的一個重要模型，因俄國數學家安德烈?馬爾科夫得名，其過程具備“無記憶”的性質，即第n+1次狀態的概率分布只跟第n次的狀態有關，與第n-1，n-2，n-3，…次狀態無關，即P（X_n+1|?，X_n-2，X_n-1，X_n）=P（X_n+1|X_n）．已知甲盒子中裝有2個黑球和1個白球，乙盒子中裝有2個白球，現從甲、乙兩個盒子中各任取一個球交換放入另一個盒子中，重復n次這樣的操作．記甲盒子中黑球個數為X_n，恰有2個黑球的概率為a_n，恰有1個黑球的概率為b_n．
  （1）求a₁，b₁和a₂，b₂；
  （2）證明：

  {

  2

  a

  n

  +

  b

  n

  -

  6

  5

  }

  為等比數列（n≥2且n∈N*）；
  （3）求X_n的期望（用n表示，n≥2且n∈N*）．
  組卷：576引用：6難度：0.6

  解析

• 22．已知拋物線C：y²=2px（p＞0），過焦點的直線l與拋物線C交于兩點A，B，當直線l的傾斜角為

  π

  6

  時，|AB|=16．
  （1）求拋物線C的標準方程和準線方程；
  （2）記O為坐標原點，直線x=-2分別與直線OA，OB交于點M，N，求證：以MN為直徑的圓過定點，并求出定點坐標．
  組卷：402引用：7難度：0.6

  解析