2013-2014學年江蘇省鹽城中學高二（下）周練數學試卷（2）

一、填空題：

• 1．高二某班共有48人，學號依次為1，2，3，…，48，現用系統抽樣的方法抽取一個容量為4的樣本，已知學號5，29，41在樣本中，那么還有一個同學的學號應為

   

  ．
  組卷：22引用：3難度：0.9

  解析

• 2．集合A={2，3}，B={1，2，3}，從A，B中各任意取一個數，則這兩數之和等于4的概率是

  ．
  組卷：50引用：9難度：0.9

  解析

• 3．在區間[-2，4]上隨機地取一個數x,若x滿足|x|≤m的概率為

  5

  6

  ，則m=

  ．
  組卷：793引用：34難度：0.7

  解析

• 4．某市連續5天測得空氣中PM2.5（直徑小于或等于2.5微米的顆粒物）的數據（單位：mg/m³）分別為115，125，132，128，125，則該組數據的方差為

  ．
  組卷：31引用：4難度：0.7

  解析

• 5．若以連續擲兩次骰子分別得到的點數m、n作為點P的坐標，則點P落在圓x²+y²=16內的概率是

  ．
  組卷：112引用：29難度：0.7

  解析

• 6．若在區間（-1，1）內任取實數a,在區間（0，1）內任取實數b,則直線ax-by=0與圓（x-1）²+（y-2）²=1相交的概率為

  ．
  組卷：77引用：16難度：0.7

  解析

二、解答題：

• 17．已知函數f（x）=x²+2ax+1（a∈R），f′（x）是f（x）的導函數．
  （1）若x∈[-2，-1]，不等式f（x）≤f′（x）恒成立，求a的取值范圍；
  （2）解關于x的方程f（x）=|f′（x）|；
  （3）設函數

  g

  （

  x

  ）

  =

  f ′ （ x ） ， f （ x ） ≥ f ′ （ x ）

  f （ x ） ， f （ x ） ＜ f ′ （ x ）

  ，求g（x）在x∈[2，4]時的最小值．
  組卷：123引用：10難度：0.1

  解析

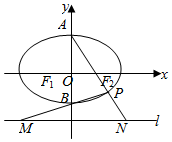• 18．如圖，橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的上、下兩個頂點為A，B，直線l：y=-2，
  點P是橢圓上異于點A、B的任意一點，連接AP并延長交直線l于點N，連接PB并延長交直線l于點M，設AP所在的直線的斜率為k₁，BP所在的直線的斜率為k₂，若橢圓的離心率為

  3

  2

  ，且過點A（0，1）．
  （1）求k₁?k₂的值及線段MN的最小值；
  （2）隨著點P的變化，以MN為直徑的圓是否恒過定點？若過定點，求出該定點；如不過定點，請說明理由．
  組卷：39引用：3難度：0.5

  解析