2022-2023學(xué)年黑龍江省哈爾濱市香坊區(qū)德強(qiáng)學(xué)校高二（上）期末數(shù)學(xué)試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知{a_n}是等差數(shù)列，且a₃+a₉=4a₅，a₂=-6，則該數(shù)列的公差是（　　）

  A．3

  B． 1 4

  C．-4

  D．-14
  組卷：233引用：5難度：0.7

  解析

• 2．已知函數(shù)f（x）的導(dǎo)函數(shù)為f'（x），且

  f

  （

  x

  ）

  =

  2

  xf

  ′

  （

  π

  6

  ）

  +

  cosx

  ，則

  f

  （

  π

  6

  ）

  =（　　）

  A． - 1 2

  B． 1 2

  C． 3 2 - π 6

  D． 3 2 + π 6
  組卷：834引用：4難度：0.7

  解析

• 3．已知F₁，F(xiàn)₂分別橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左右焦點，P為橢圓上一點，滿足∠PF₂F₁=

  π

  2

  ，線段PF₁交y軸于點Q，若|QF₂|=

  2

  c,則橢圓的離心率是（　　）

  A． 1 2

  B． 2 2

  C． 1 + 2 3

  D． 2 - 1
  組卷：466引用：3難度：0.7

  解析

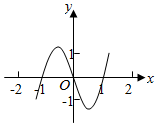• 4．已知函數(shù)y=xf′（x）的圖象如圖所示（其中f′（x）是函數(shù)f（x）的導(dǎo)函數(shù)），下面四個圖象中，y=f（x）的圖象大致是（　　）

  A．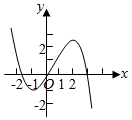

  B．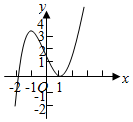

  C．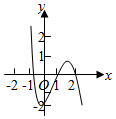

  D．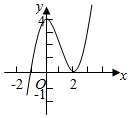
  組卷：918引用：55難度：0.9

  解析

• 5．已知一個乒乓球從h米高的高度自由落下，每次落下后反彈的高度是原來高度的m（0＜m＜1）倍，則當(dāng)它第2023次著地時，經(jīng)過的總路程是（　　）

  A． h + 2 hm （ 1 - m 2023 ） 1 - m	B．h + 2 hm （ 1 - m 2022 ） 1 - m
  C．h + hm （ 1 - m 2023 ） 1 - m	D． h + hm （ 1 - m 2022 ） 1 - m
  組卷：29引用：1難度：0.6

  解析

• 6．古印度數(shù)學(xué)家婆什伽羅在《麗拉沃蒂》一書中提出如下問題：某人給一個人布施，初日施2子安貝（古印度貨幣單位），以后逐日倍增，問一月共施幾何？在這個問題中，以一個月31天計算，記此人第n日布施了a_n子安貝（其中1≤n≤31，n∈N^*），數(shù)列{a_n}的前n項和為S_n．若關(guān)于n的不等式

  S

  n

  -

  62

  ＜

  a

  2

  n

  +

  1

  -

  t

  a

  n

  +

  1

  恒成立，則實數(shù)t的取值范圍為（　　）

  A．（-∞，7）

  B．（-∞，15）

  C．（-∞，16）

  D．（-∞，32）
  組卷：53引用：3難度：0.6

  解析

• 7．對于函數(shù)f（x）=sinx+x-e^x，x∈[0，π]，下列說法正確的是（　　）

  A．函數(shù)f（x）有唯一的極大值點

  B．函數(shù)f（x）有唯一的極小值點

  C．函數(shù)f（x）有最大值沒有最小值

  D．函數(shù)f（x）有最小值沒有最大值
  組卷：283引用：5難度：0.6

  解析

三、解答題：共70分．解答應(yīng)寫出文字說明、解答過程或演算步驟．

• 21．已知拋物線C：y²=2px（p＞0）的焦點為F，拋物線上的點P到y(tǒng)軸的距離等于|PF|-1．
  （1）求p的值；
  （2）是否存在正數(shù)m,對于過點M（m,0）且與拋物線C有兩個交點A、B的任一直線，都有

  FA

  ?

  FB

  ＜0？若存在，求出m的取值范圍；若不存在，請說明理由．
  組卷：69引用：3難度：0.3

  解析

• 22．設(shè)函數(shù)u（x）=lnx-ax+a,函數(shù)v（x）=

  1

  2

  x²-axlnx+a（a∈R）．
  （1）求u（x）的單調(diào)區(qū)間；
  （2）若f（x）=v（x）-u（x），g（x）=f'（x）=0有三個不同實根x₁，x₂，x₃（x₁＜x₂＜x₃），試比較f（x₁），f（x₂），f（x₃）的大小關(guān)系，并說明理由．
  組卷：185引用：3難度：0.1

  解析