當前位置：試卷中心 > 試卷詳情

2023-2024學年海南省瓊海市海桂中學高二（上）第一次月考數學試卷

發布：2024/9/23 13:0:11

1．已知集合A={x|-1≤x≤2}，B={x|x＞0}，則A∪B=（　　）
A．{x|x≤2} B．{x|x≥-1} C．{x|x＞1} D．{x|x＞0}
組卷：220引用：8難度：0.9
解析
2．（1+2i）（2+i）=（　　）
A．4+5i B．5i C．-5i D．2+3i
組卷：2351引用：7難度：0.9
解析
3．已知點A（2，0），
B
（
3
，
3
）
，則直線AB的傾斜角為（　　）
A．30° B．60° C．120° D．150°
組卷：164引用：6難度：0.8
解析
4．已知
a
=
（
1
，-
2
，
1
）
，
b
=
（
-
1
，
2
，
3
）
，則
2
a
?
b
=（　　）
A．-4 B．-3 C．-2 D．-1
組卷：87引用：4難度：0.8
解析
5．已知兩個向量
a
=
（
2
，-
1
，
3
）
，
b
=
（
4
，
m
,
n
）
，且
a
∥
b
，則m+n的值為（　　）
A．1 B．2 C．4 D．8
組卷：488引用：29難度：0.9
解析
6．如圖，在正方體ABCD-A₁B₁C₁D₁中，點E是上底面A₁B₁C₁D₁的中心，則異面直線AE與BD₁所成角的余弦值為（　　）
A．
2
4
B．
2
3
C．
10
4
D．
6
3
組卷：113引用：14難度：0.6
解析
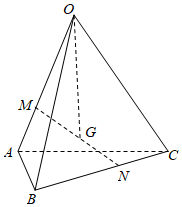7．如圖在四面體OABC中，M，N分別在棱OA，BC上且滿足
OM
=
2
MA
，
BN
=
2
NC
，點G是線段MN的中點，用向量
OA
，
OB
，
OC
表示向量
OG
應為（　　）
A．
OG
=
1
3
OA
+
1
6
OB
+
1
3
OC
B．
OG
=
1
3
OA
+
1
3
OB
+
1
6
OC
C．
OG
=
1
3
OA
+
1
4
OB
+
1
4
OC
D．
OG
=
1
4
OA
+
1
4
OB
+
1
3
OC
組卷：508引用：10難度：0.8
解析

21．如圖，幾何體ABCD-A₁C₁D₁為直四棱柱ABCD-A₁B₁C₁D₁截去一個角所得，四邊形ABCD是正方形，AB=2，DD₁=3，P為BC的中點．
（1）證明：平面A₁BC₁∥平面ACD₁；
（2）求平面D₁DP與平面A₁BC₁所成銳二面角的余弦值．
組卷：28引用：1難度：0.5
解析
22．如圖，三棱錐P-ABC中，底面△ABC是邊長為2的正三角形，PA=2，PA⊥底面ABC，點E，F分別為AC，PC的中點．
（1）求證：平面BEF⊥平面PAC；
（2）在線段PB上是否存在點G，使得直線AG與平面PBC所成的角的余弦值為
42
7
？若存在，確定點G的位置；若不存在，請說明理由．
組卷：130引用：2難度：0.7
解析

A． OG = 1 3 OA + 1 6 OB + 1 3 OC	B． OG = 1 3 OA + 1 3 OB + 1 6 OC
C． OG = 1 3 OA + 1 4 OB + 1 4 OC	D． OG = 1 4 OA + 1 4 OB + 1 3 OC

1．已知集合A={x|-1≤x≤2}，B={x|x＞0}，則A∪B=（ ）