2022-2023學(xué)年湖南省邵陽市邵東一中高一（下）第一次月考數(shù)學(xué)試卷

一、選擇題（共8小題，每小題5分，滿分40分）

• 1．設(shè)集合A={x|x＜x²}，B={x|x²+x-6＜0}，則A∩B=（　　）

  A．（0，1）	B．（-2，0）∪（1，3）
  C．（-3，1）	D．（-3，0）∪（1，2）
  組卷：86引用：6難度：0.8

  解析

• 2．下列能化簡為

  PQ

  的是（　　）

  A． QC - QP + CQ	B． AB + （ PA + BQ ）
  C． （ AB + PC ） + （ BA - QC ）	D． PA + AB - BQ
  組卷：450引用：9難度：0.8

  解析

• 3．命題?x∈R，e^x-x-1≥0的否定是（　　）

  A．?x∈R，ex-x-1≤0	B．?x∈R，ex-x-1≥0
  C．?x0∈R，ex0-x0-1≤0	D．?x0∈R，ex0-x0-1＜0
  組卷：154引用：5難度：0.8

  解析

• 4．已知a=log₂0.2，b=2^0.2，c=0.2^0.3，則（　　）

  A．a(chǎn)＜b＜c

  B．a(chǎn)＜c＜b

  C．c＜a＜b

  D．b＜c＜a
  組卷：3560引用：117難度：0.9

  解析

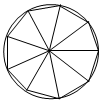• 5．劉徽（約公元225年-295年），魏晉期間偉大的數(shù)學(xué)家，中國古典數(shù)學(xué)理論的奠基人之一他在割圓術(shù)中提出的，”割之彌細(xì)，所失彌少，割之又割，以至于不可割，則與圓周合體而無所失矣”，這可視為中國古代極限觀念的佳作，割圓術(shù)的核心思想是將一個圓的內(nèi)接正n邊形等分成n個等腰三角形（如圖所示），當(dāng)n變得很大時，這n個等腰直角三角形的面積之和近似等于圓的面積，運用割圓術(shù)的思想，得到sin2°的近似值為（　　）

  A． π 90

  B． π 180

  C． π 270

  D． π 360
  組卷：128引用：11難度：0.8

  解析

• 6．已知函數(shù)

  f

  （

  x

  ）

  =

  （ a + 2 ） x , （ x ≤ 1 ）

  x a - 6 ， （ x ＞ 1 ）

  是減函數(shù)，則實數(shù)a的取值范圍是（　　）

  A．[-7，-2）

  B．（-∞，-2）

  C．（-∞，-7）

  D．（-7，-2）
  組卷：114引用：3難度：0.7

  解析

• 7．設(shè)向量

  a

  與

  b

  滿足

  |

  a

  |

  =

  2

  ，

  b

  在

  a

  方向上的投影向量為

  -

  1

  2

  a

  ，若存在實數(shù)λ，使得

  a

  與

  a

  -

  λ

  b

  垂直，則λ=（　　）

  A．2

  B．-2

  C． 3

  D． - 3
  組卷：229引用：6難度：0.7

  解析

四、解答題（共6小題，滿分70分）

• 21．已知函數(shù)f（x）=

  a

  |

  x

  |

  -

  1

  |

  x

  |

  ．
  （1）寫出函數(shù)f（x）的單調(diào)區(qū)間；
  （2）若f（x）＜2x在（1，+∞）恒成立，求實數(shù)a的取值范圍；
  （3）若函數(shù)y=f（x）在[m,n]上值域是[m,n]（m≠n），求實數(shù)a的取值范圍．
  組卷：12引用：2難度：0.4

  解析

• 22．已知函數(shù)f（x）=log_a（x+2）（a＞0且a≠1），g（x）=cos（πx）．
  （1）求不等式f（x）≥1的解集；
  （2）若函數(shù)f（x）過點（7，2），并且函數(shù)F（x）=f（x）+k?g（x）（k∈R）滿足F（-1）=-2，求實數(shù)a與k的值；
  （3）在（2）的條件下，判斷函數(shù)F（x）在[-1，0]上的單調(diào)性（不必說明理由）．若a∈[0，1]時，不等式F（

  a

  2

  +

  1

  2

  sin2x-1）-F（a（sinx-cosx））＜0對任意x∈[0，

  π

  4

  ]恒成立，求實數(shù)a的取值范圍．
  組卷：67引用：4難度：0.2

  解析