2023-2024學年云南省昆明市官渡二中高三（上）期初數學試卷

一、選擇題；本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設集合A={x|-1≤x＜1}，Z為整數集，則A∩Z=（　　）

  A．{-1，0}

  B．{-1，1}

  C．{0，1}

  D．{-1，0，1}
  組卷：37引用：3難度：0.9

  解析

• 2．在復平面內，復數z對應的點為（-1，2），則

  z

  -

  i

  1

  +

  i

  =（　　）

  A．1

  B．i

  C．-i

  D． - 3 2 - 5 2 i
  組卷：40引用：5難度：0.8

  解析

• 3．已知方程（x²-mx+27）（x²-nx+27）=0的四個根組成以1為首項的等比數列，則|m-n|=（　　）

  A．8

  B．12

  C．16

  D．20
  組卷：290引用：5難度：0.7

  解析

• 4．若

  sinθ

  =

  5

  cosθ

  ，則tan2θ=（　　）

  A．- 5 3

  B． 5 3

  C．- 5 2

  D． 5 2
  組卷：1024引用：6難度：0.7

  解析

• 5．已知橢圓E：

  x

  2

  11

  +

  y

  2

  2

  =

  1

  與雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  5

  =

  1

  （a＞0，b＞0）有相同的焦點，則雙曲線C的漸近線方程為（　　）

  A． y =± 3 5 5 x

  B． y =± 5 3 x

  C． y =± 2 5 5 x

  D． y =± 5 2 x
  組卷：180引用：9難度：0.7

  解析

• 6．已知f（x）是定義在R上的偶函數，其圖象關于點（1，0）對稱．以下關于f（x）的結論：
  ①f（x）是周期函數；
  ②f（x）滿足f（x）=f（4-x）；
  ③f（x）在（0，2）單調遞減；
  ④f（x）=cos

  πx

  2

  是滿足條件的一個函數，
  其中正確結論的個數是（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：68引用：2難度：0.6

  解析

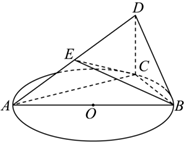• 7．如圖，△ABC內接于圓O，AB為圓O的直徑，AB=5，BC=3，CD⊥平面ABC，E為AD的中點，且異面直線BE與AC所成角為60°，則點A到平面BCE的距離為（　　）

  A． 8 21 3

  B． 8 7 7

  C． 4 21 7

  D． 4 7 3
  組卷：136引用：3難度：0.5

  解析

四、解答題；本題共6個小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

• 21．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  5

  5

  ，短軸長為4．
  （1）求C的標準方程；
  （2）過C的左焦點F作相互垂直的兩條直線l₁，l₂（均不垂直于x軸），l₁交C于A，B兩點，l₂交C于C，D兩點．設線段AB，CD的中點分別為P，Q，證明：直線PQ恒過x軸上一定點．
  組卷：13引用：2難度：0.5

  解析

• 22．已知函數f（x）=1-x-axlnx（a∈R），g（x）=

  f

  （

  x

  ）

  x

  +

  1

  ．
  （1）當a=-

  1

  2

  時，求f（x）的最小值；
  （2）當0＜a≤1時，g（x）≤m恒成立，求整數m的最小值．
  組卷：135引用：2難度：0.6

  解析