2023-2024學年河南省信陽市羅山縣八年級（上）期中數學試卷

一、選擇題（每小題3分，共30分）

• 1．第19屆亞運會將于2023年9月在杭州舉行，下列歷屆亞運會會徽是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：265引用：15難度：0.9

  解析

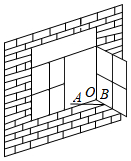• 2．如圖，一扇窗戶打開后用窗鉤AB可將其固定，這里所運用的幾何原理（　　）

  A．兩點確定一條直線

  B．垂線段最短

  C．三角形具有穩定性

  D．三角形的內角和等于180°
  組卷：39引用：3難度：0.9

  解析

• 3．如圖，BD是∠ABC的角平分線，DE⊥AB于E，△ABC的面積是30cm²，AB=12cm,DE=3cm,則BC的長度為（　　）

  A．6cm

  B．7cm

  C．8cm

  D．9cm
  組卷：91引用：2難度：0.5

  解析

• 4．如圖，在△ABC中，按以下步驟作圖：①分別以B，C為圓心，大于

  1

  2

  BC的長為半徑作弧，兩弧相交于點M，N；②作直線MN交AB于點D，交BC于點E，連接CD．下列說法不確定的是（　　）

  A．BE=CE

  B．BD=CD

  C．ME=EN

  D．CD=CA
  組卷：42引用：3難度：0.5

  解析

• 5．已知△ABC的六個元素，則甲、乙、丙三個三角形中與△ABC全等的是（　　）
  

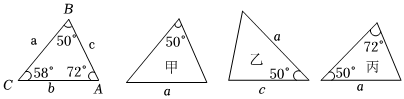
  A．乙

  B．甲、丙

  C．乙、丙

  D．丙
  組卷：99引用：2難度：0.7

  解析

• 6．“三等分角”大約是在公元前五世紀由古希臘人提出來的，借助如圖所示的“三等分角儀”能三等分任一角．這個三等分角儀由兩根有槽的棒OA，OB組成，兩根棒在O點相連并可繞O轉動、C點固定，OC=CD=DE，點D、E可在槽中滑動．若∠BDE=75°，則∠CDE的度數是（　　）
  

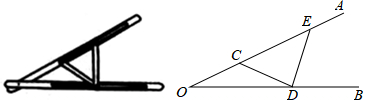
  A．60°

  B．65°

  C．75°

  D．80°
  組卷：5978引用：103難度：0.8

  解析

• 7．下列結論不一定正確的是（　　）

  A．三角形的中線、角平分線、高都是線段

  B．任意多邊形的外角和都是360°

  C．從n邊形的一個頂點出發，可以作（n-3）條對角線

  D．三角形三條角平分線的交點到各頂點的距離相等
  組卷：67引用：2難度：0.8

  解析

三、解答題（本題8個小題，滿分75分）

• 22．如果一個三角形能被一條線段分割成兩個等腰三角形，那么稱這條線段為這個三角形的內好線，稱這個三角形為內好三角形．
  
  （1）如圖1，△ABC是等腰銳角三角形，AB=AC（AB＞BC），若∠ABC的角平分線BD交AC于點D，且BD是△ABC的一條內好線，則∠BDC=

  度；
  （2）如圖2，△ABC中，∠B=2∠C，線段AC的垂直平分線交AC于點D，交BC于點E．求證：AE是ABC的一條內好線；
  （3）如圖3，已知△ABC是內好三角形，且∠A=24°，∠B為鈍角，則所有可能的∠B的度數為

  （直接寫答案）．
  組卷：1065引用：13難度：0.2

  解析

• 23．回答問題
  （1）【初步探索】如圖1，在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分別是BC、CD上的點，且EF=BE+FD，探究圖中∠BAE、∠FAD、∠EAF之間的數量關系，小王同學探究此問題的方法是：延長FD到點G，使DG=BE，連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論是

  ；
  （2）【靈活運用】如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，E、F分別是BC、CD上的點，且EF=BE+FD，上述結論是否仍然成立，并說明理由；
  （3）【拓展延伸】已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD，若點E在CB的延長線上，點F在CD的延長線上，如圖3，仍然滿足EF=BE+FD，請直接寫出∠EAF與∠DAB的數量關系．
  
  組卷：1071引用：9難度：0.3

  解析