當前位置：試卷中心 > 試卷詳情

2023-2024學年江蘇省南京第五高級中學高二（上）月考數學試卷（10月份）

發布：2024/9/13 14:0:9

一、單選題（共8小題，每小題5分，共40分.）

1．雙曲線
x
2
4
-y²=1的頂點到其漸近線的距離等于（　　）
A．
2
5
5
B．1 C．
4
5
5
D．2
組卷：184引用：8難度：0.9
解析
2．古希臘數學家阿波羅尼斯在其巨著《圓錐曲線論》中提出“在同一平面上給出三點，若其中一點到另外兩點的距離之比是一個大于零且不等于1的常數，則該點軌跡是一個圓”．現在，某電信公司要在甲、乙、丙三地搭建三座5G信號塔來構建一個特定的三角形信號覆蓋區域，以實現5G商用，已知甲、乙兩地相距4km,丙、甲兩地距離是丙、乙兩地距離的
3
倍，則這個三角形信號覆蓋區域的最大面積（單位：km²）是（　　）
A．
2
3
B．
4
3
C．
3
6
D．
4
6
組卷：77引用：3難度：0.5
解析
3．若拋物線x²=12y的焦點與雙曲線
y
2
a
2
-
x
2
5
=1的一個焦點重合，則此雙曲線的漸近線方程為（　　）
A．y=±
5
2
x B．y=±
5
4
x C．y=±
2
5
5
x D．y=±
4
5
x
組卷：155引用：6難度：0.7
解析
4．拋物線C：y²=2px（p＞0）的焦點為F，過F與x軸垂直的直線交C于點M，N，有下列四個命題：
甲：點F坐標為（1，0）；
乙：拋物線C的準線方程為x=-2；
丙：線段MN長為4；
丁：直線y=x+1與拋物線C相切．
如果只有一個命題是假命題，則該命題是（　　）
A．甲 B．乙 C．丙 D．丁
組卷：102引用：4難度：0.7
解析
5．如圖所示，一隧道內設雙行線公路，其截面由一個長方形和拋物線構成，為保證安全，要求行駛車輛頂部（設為平頂）與隧道頂部在豎直方向上高度之差至少要有0.5m,已知行車道總寬度AB=6m,那么車輛通過隧道的限制高度為（　　）
A．2.25m B．2.5m C．3.25m D．3.5m
組卷：88引用：2難度：0.5
解析
6．已知F₁，F₂是橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點，點P在橢圓C上，線段PF₂與圓x²+y²=b²相切于點Q，且點Q為線段PF₂的中點，則
5
a
2
+
2
e
2
3
b
（其中e為橢圓C的離心率）的最小值為（　　）
A．
5
3
3
B．
5
2
3
C．
5
D．
2
5
3
組卷：385引用：2難度：0.5
解析
7．油紙傘是中國傳統工藝品，至今已有1000多年的歷史，為宣傳和推廣這一傳統工藝，北京市文化宮開展油紙傘文化藝術節．活動中，某油紙傘撐開后擺放在戶外展覽場地上，如圖所示，該拿傘沿是一個半徑為2的圓，圓心到傘柄底端距離為2，當陽光與地面夾角為60°時，在地面形成了一個橢圓形影子，且傘柄底端正好位于該橢圓的長軸上，若該橢圓的離心率為e,則e²=（　　）
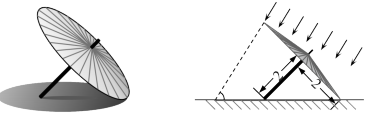
A．
1
9
B．7-2
3
C．3-2
2
D．3
3
-5
組卷：285引用：18難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共6小題，17題10分，18-22題各12分，共70分。）

21．給定橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，稱圓心在原點O、半徑是
a
2
+
b
2
的圓為橢圓C的“準圓”．已知橢圓C的一個焦點為
F
（
2
，
0
）
，其短軸的一個端點到點F的距離為
3
．
（1）求橢圓C和其“準圓”的方程；
（2）若點A是橢圓C的“準圓”與x軸正半軸的交點，B、D是橢圓C上的兩相異點，且BD⊥x軸，求
AB
?
AD
的取值范圍．
組卷：84引用：5難度：0.5
解析
22．已知兩圓
C
1
：
（
x
-
2
）
2
+
y
2
=
18
，
C
2
：
（
x
+
2
）
2
+
y
2
=
2
，動圓M在圓C₁內部且和圓C₁內切，和圓C₂外切．
（1）求動圓圓心M的軌跡方程C；
（2）是否存在圓心在原點的圓，使得該圓的任意一條切線與軌跡方程C恒有兩個交點M、N，且滿足OM⊥ON？若存在，求出該圓的方程，若不存在，說明理由．
組卷：107引用：4難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2023-2024學年江蘇省南京第五高級中學高二（上）月考數學試卷（10月份）

一、單選題（共8小題，每小題5分，共40分.）

1．雙曲線x24-y2=1的頂點到其漸近線的距離等于（ ）

3．若拋物線x2=12y的焦點與雙曲線y2a2-x25=1的一個焦點重合，則此雙曲線的漸近線方程為（ ）

6．已知F1，F2是橢圓C：x2a2+y2b2=1（a＞b＞0）的左、右焦點，點P在橢圓C上，線段PF2與圓x2+y2=b2相切于點Q，且點Q為線段PF2的中點，則5a2+2e23b（其中e為橢圓C的離心率）的最小值為（ ）

四、解答題（共6小題，17題10分，18-22題各12分，共70分。）

1．雙曲線
x
2
4
-y²=1的頂點到其漸近線的距離等于（　　）

3．若拋物線x²=12y的焦點與雙曲線
y
2
a
2
-
x
2
5
=1的一個焦點重合，則此雙曲線的漸近線方程為（　　）

6．已知F₁，F₂是橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點，點P在橢圓C上，線段PF₂與圓x²+y²=b²相切于點Q，且點Q為線段PF₂的中點，則
5
a
2
+
2
e
2
3
b
（其中e為橢圓C的離心率）的最小值為（　　）