2022-2023學(xué)年河南省信陽(yáng)市百師聯(lián)盟高一（下）期中數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是待合題目要求的．

• 1．集合A={x|x²-2x-3＜0}，B={-2，-1，0，2，4}，則（?_RA）∩B=（　　）

  A．{-2，-1，4}

  B．{-1，2}

  C．{-2，4}

  D．?
  組卷：83引用：2難度：0.7

  解析

• 2．已知命題p：?x∈R，x²＜0，則￢p是（　　）

  A．?x∈R，x2≥0	B．?x0∈R， x 2 0 ≥ 0
  C．?x?R， x 2 0 ≥ 0	D．?x0∈R， x 2 0 ＞ 0
  組卷：109引用：3難度：0.8

  解析

• 3．已知i為虛數(shù)單位，復(fù)數(shù)z₁=1+2i,z₂=2-i,則（　　）

  A．z1的共軛復(fù)數(shù)為-1+2i	B．z1的虛部是2i
  C．z1+z2為實(shí)數(shù)	D．z1z2=4+3i
  組卷：32引用：2難度：0.8

  解析

• 4．設(shè)點(diǎn)A，B，C不共線，則“

  |

  AB

  +

  AC

  |

  ＜

  |

  BC

  |

  ”是“

  AB

  與

  AC

  的夾角為鈍角”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：244引用：5難度：0.5

  解析

• 5．下列說(shuō)法正確的是（　　）

  A．過(guò)空間中的任意三點(diǎn)有且只有一個(gè)平面

  B．三棱柱各面所在平面將空間分成21部分

  C．空間中的三條直線a,b,c,如果a與b異面，b與c異面，那么a與c異面

  D．若直線a在平面α外，則平面α內(nèi)存在直線與a平行
  組卷：74引用：4難度：0.7

  解析

• 6．函數(shù)f（x）=sin（2ωx+φ）（x∈R，ω＞0，0≤φ＜2π）的部分圖像如圖，則（　　）

  A． ω = π 8 ， φ = 5 π 4

  B． ω = π 8 ， φ = π 4

  C． ω = π 4 ， φ = π 4

  D． ω = π 6 ， φ = π 6
  組卷：111引用：2難度：0.7

  解析

• 7．設(shè)

  y

  =

  1

  x

  +

  1

  2

  -

  x

  ，x∈[1，2），則y的最小值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：544引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

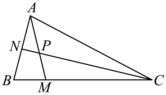• 21．已知在△ABC中，點(diǎn)M是BC邊上靠近點(diǎn)B的四等分點(diǎn)，點(diǎn)N在AB邊上，且

  AN

  =

  NB

  ，設(shè)AM與CN相交于點(diǎn)P．記

  AB

  =

  m

  ，

  AC

  =

  n

  ．
  （1）請(qǐng)用

  m

  ，

  n

  表示向量

  AM

  ；
  （2）若

  |

  n

  |

  =

  2

  |

  m

  |

  ，設(shè)

  m

  ，

  n

  的夾角為θ，若

  cosθ

  =

  1

  4

  ，求證：

  CN

  ⊥

  AB

  ．
  組卷：174引用：7難度：0.7

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  lo

  g

  2

  [

  （

  2

  -

  a

  ）

  2

  x

  +

  1

  ]

  -

  x

  ，函數(shù)g（x）=2^-x-t?2^x．
  （1）若g（x）是偶函數(shù)，求實(shí)數(shù)t的值，并用單調(diào)性的定義判斷g（x）在[0，+∞）上的單調(diào)性；
  （2）在（1）的條件下，若對(duì)于?x₁∈[0，+∞），?x₂∈R，都有f（x₁）+2≤g（x₂）+log₂2a成立，求實(shí)數(shù)a的取值范圍．
  組卷：29引用：2難度：0.4

  解析