2022-2023學年河北省金科大聯考高一（上）期中數學試卷

一、單項選擇題:本題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。

• 1．下列圖形能表示函數圖象的是（　　）

  A．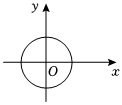

  B．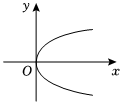

  C．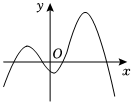

  D．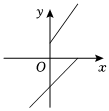
  組卷：279引用：2難度：0.8

  解析

• 2．函數f（x）=

  4

  x

  -

  x

  2

  +（x-2）⁰的定義域為（　　）

  A．（0，4）	B．[0，2）∪（2，4]
  C．[0，4]	D．（0，2）∪（2，4）
  組卷：87引用：5難度：0.8

  解析

• 3．下列命題為真命題的是（　　）

  A．若a∈N，則-a?N

  B．集合{x|x2-6x+9=0}有兩個真子集

  C．若x=y,則 x = y

  D．不存在奇數的立方是偶數
  組卷：33引用：1難度：0.7

  解析

• 4．已知集合A={x|-3＜x＜2}，集合B={x|0＜x＜5}，則圖中陰影部分表示的集合為（　　）

  A．{x|-3＜x＜5}	B．{x|0＜x＜2}
  C．{x|-3＜x≤0}	D．{x|-3＜x≤0或2≤x＜5}
  組卷：82引用：10難度：0.7

  解析

• 5．已知命題“?x∈R，使（m-2）x²+（m-2）x+1≤0”是假命題，則實數m的取值范圍為（　　）

  A．m＞6

  B．2＜m＜6

  C．2≤m＜6

  D．m≤2
  組卷：748引用：12難度：0.7

  解析

• 6．定義在R上的偶函數f（x）滿足：對任意的x₁，x₂∈（-∞，0]（x₁≠x₂），有（x₁-x₂）?[f（x₁）-f（x₂）]＜0，則（　　）

  A．f（-1）＜f（π）＜f（4）	B．f（-1）＞f（π）＞f（4）
  C．f（π）＜f（4）＜f（-1）	D．f（4）＜f（-1）＜f（π）
  組卷：22引用：3難度：0.7

  解析

• 7．對于實數x,規定[x]表示不大于x的最大整數，例如[1.5]=1，[3.9]=3，[-2.5]=-3，[5]=5，那么使得不等式6[x]²-5[x]-21＜0成立的x的取值范圍是（　　）

  A．-2≤x＜3

  B．-1＜x＜3

  C．-1≤x≤2

  D．-1≤x＜3
  組卷：35引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分。解答應寫出必要的文字說明、證明過程及演算步驟。

• 21．2022年2月4日北京冬奧會在全世界的矚目下拉開大幕，北京成為了迄令為止，世界上第一個雙奧之城，北京冬奧會的吉祥物“冰墩墩”寓意創造非凡，探索未來，更是受到了各國友人的搶購，造成了一墩難求的局面，某冬奧官方紀念品銷售處在2022年1月累計銷量突破了40萬件．現某企業計劃引進新的生產設備和新的產品方案，通過市場分析，2022年2月每生產x（萬件）獲利W（x）（萬元），W（x）=

  20 （ x 2 + 17 ） ， 0 ＜ x ≤ 2

  500 - 80 x - 1 ， 2 ＜ x ≤ 5

  該公司預計2022年2月這個新產品的其他成本總投入為（20x+10）萬元，由市場調研分析得知，當前該產品的冰墩墩供不應求．記該企業2022年2月的利潤為f（x）（單位：萬元）．
  （1）求函數f（x）的解析式；
  （2）當2022年2月該產品的冰墩墩的產量為多少萬件時，該企業2月的利潤最大？最大利潤是多少？請說明理由．
  組卷：93引用：4難度：0.6

  解析

• 22．已知函數f（x）=

  1

  +

  x

  ，g（x）=

  1

  -

  x

  ．
  （1）求函數h（x）=f（x）+g（x）的值域；
  （2）已知a為實數，函數m（x）=af（x）g（x）+f（x）+g（x）的最大值為F（a），求F（a）．
  組卷：64引用：2難度：0.4

  解析