2021-2022學年四川省成都市蓉城名校聯盟高二（下）期末數學試卷（理科）

一、選擇題:本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設集合A={x||x|≤1}，B={x|x²-2x＜0}，則A∪B=（　　）

  A．[0，1）

  B．[-1，2）

  C．[0，2）

  D．[1，2）
  組卷：545引用：2難度：0.8

  解析

• 2．已知i為虛數單位，復數z滿足z（1-i）=4+3i,則|z|=（　　）

  A． 10 2

  B． 5 2

  C． 5 2 2

  D． 7 2
  組卷：89引用：2難度：0.8

  解析

• 3．命題“?x∈R，e^x≥lnx+2”的否定是（　　）

  A．?x0∈R，e x 0 ＜lnx0+2	B．?x∈R，ex＜lnx+2
  C．?x0∈R，e x 0 ≥lnx0+2	D．?x0?R，e x 0 ＜lnx0+2
  組卷：94引用：3難度：0.8

  解析

• 4．在等差數列{a_n}中，已知a₄=3，a₂+a₈=10，則數列{a_n}的公差為（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：175引用：2難度：0.8

  解析

• 5．設x,y滿足約束條件

  2 x - 3 ≤ y

  x + y ≥ 1

  y ≤ 3

  ，則z=x+2y的最大值為（　　）

  A．3

  B．5

  C．7

  D．9
  組卷：45引用：3難度：0.7

  解析

• 6．若函數f（x）=

  2 lnx , x ＞ 0

  x 2 - 1 ， x ≤ 0

  ，則f[f（

  1

  e

  ）]=（　　）

  A．3

  B． 1 e 2 -1

  C．e2-1

  D．8
  組卷：64引用：2難度：0.8

  解析

• 7．執行如圖所示的程序框圖，如果輸入n=5，則輸出的S值為（　　）
  

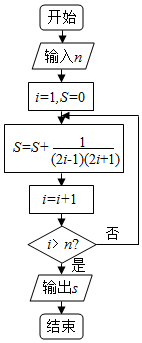
  A． 4 9

  B． 8 9

  C． 5 11

  D． 10 11
  組卷：41引用：5難度：0.9

  解析

三、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知橢圓C：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  的右焦點為F，過點F的直線（不與x軸垂直）與橢圓C相交于A，B兩點，直線l：x=4與x軸相交于點H，過點A作AD⊥l,垂足為D．
  （1）求四邊形OAHB（O為坐標原點）面積的取值范圍；
  （2）證明：直線BD過定點E，并求點E的坐標．
  組卷：108引用：2難度：0.5

  解析

• 22．在直角坐標系xOy中，曲線C₁的參數方程為

  x = 1 + 2 t

  y = 2 3 t

  （t為參數），以坐標原點為極點，以x軸正半軸為極軸建立極坐標系，曲線C₂的極坐標方程為ρ²=

  2

  2

  -

  co

  s

  2

  θ

  ．
  （1）求曲線C₁的極坐標方程和曲線C₂的直角坐標方程；
  （2）若曲線C₁與C₂交于A，B兩點，且點P（1，0），求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  的值．
  組卷：82引用：2難度：0.5

  解析